思维之海

——在云端，寻找我的星匙。

深度学习训练营

In

深度学习训练营课程笔记。

References

机器学习初等指南(1)

机器学习初等指南(2)

机器学习初等指南(3)

参考课件.zip

AI研习社

深度学习Tensorflow相关书籍推荐和PDF下载

深度学习入门：基于Python的理论与实现

逻辑回归

逻辑回归的内容可以回顾这里：机器学习初等指南(1)-逻辑回归。

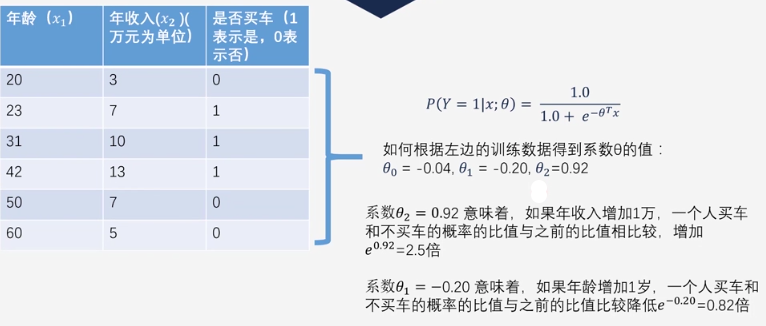
Ex：利用年龄和收入预测是否买车。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn import linear_model #引入sklearn线性模型

X = [[20, 3],
	[23, 7],
	[31, 10],
	[42, 13],
	[50, 7],
	[60, 5]]  #年龄-收入矩阵
y = [0, 1, 1, 1 ,0 , 0] #观测向量

lr = linear_model.LogisticRegression() #创建对象
lr.fit(X,y) #获得拟合参数

testX = [[28, 8]] #测试集（矩阵）

label = lr.predict(testX) #预测
print("predicted Label = ", label)
prob = lr.predict_proba(testX) #预测概率
print("probability = ", prob)

拟合系数的含义

则概率比值$odds=\frac{p}{1-p}=e^{\theta^Tx}$。

$系数\theta_j意味着，假设odds为\lambda_1(原),\lambda_2(新)，若x_j增加1，有\cfrac{\lambda_2}{\lambda_1}=e^{\theta_j}$。

以下是验证程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from sklearn import linear_model #引入sklearn线性模型

X = [[20, 3],
	[23, 7],
	[31, 10],
	[42, 13],
	[50, 7],
	[60, 5]]  #年龄-收入矩阵
y = [0, 1, 1, 1 ,0 , 0] #观测向量
lr = linear_model.LogisticRegression()
lr.fit(X,y) #获得拟合参数

testX = [[28, 8]] #测试集（矩阵）

label = lr.predict(testX) #预测
print("predicted Label = ", label)

prob = lr.predict_proba(testX) #预测概率
print("probability = ", prob)
#-----------------------------------------以下是新增部分
theta_0 = lr.intercept_
theta_1 = lr.coef_[0][0]
theta_2 = lr.coef_[0][1]
print("theta_0 = ", theta_0)
print("theta_1 = ", theta_1)
print("theta_2 = ", theta_2)

ratio = prob[0][1]/prob[0][0]

testX = [[28, 9]]
prob_new = lr.predict_proba(testX)
ratio_new = prob_new[0][1]/prob_new[0][0]

ratio_of_ratio = ratio_new / ratio
print("ratio_of_ratio = ", ratio_of_ratio)

import math
theta_2_exp = math.exp(theta_2)
print("theta_2_exp = ", theta_2_exp)

应用案例

参考程序：spam_detection.ipynb， 垃圾短信检测数据集.zip

示例代码

在hexo中写的文章支持jupyter-notebook显示| 幻悠尘的小窝

注意需要npm install co。

太偏右修正：https://github.com/qiliux/hexo-jupyter-notebook/issues/3。

核心代码：document.getElementById('ipynb').style['margin-left'] = '-60px';

简单代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import pandas as pd
from sklearn import linear_model
from sklearn.feature_extraction.text import TfidfVectorizer

df = pd.read_csv('spam.csv', delimiter=',', header=None, encoding='latin-1')
print(df.head(5))
y, X_train = df[0], df[1] 
# df = pd.read_csv('spam.csv', delimiter=',', encoding='latin-1')
# y, X_train = df.iloc[:,0], df.iloc[:,1]

vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(X_train)

lr = linear_model.LogisticRegression()
lr.fit(X, y)

testX = vectorizer.transform(['URGENT! Your mobile No. 1234 was awarded a prize.',
							  'Hey honey, whats up?'])
predictions = lr.predict(testX)
print(predictions)

神经网络

神经网络的内容可以回顾这里：机器学习初等指南(2)。

鸢尾花分类

鸢尾花数据集， Iris flower data set

https://raw.githubusercontent.com/uiuc-cse/data-fa14/gh-pages/data/iris.csv

探索sklearn | 鸢尾花数据集

机器学习iris数据集导入

【python数据挖掘课程】十九.鸢尾花数据集可视化、线性回归、决策树花样分析

Iris鸢尾花数据集可视化、线性回归、决策树分析、KMeans聚类分析

Iris plants 数据集可以从KEEL dataset数据集网站获取，也可以直接从Sklearn.datasets机器学习包得到。数据集共包含4个特征变量、1个类别变量，共有150个样本。类别变量分别对应鸢尾花的三个亚属，分别是山鸢尾 (Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica) 分别用[0,1,2]来做映射。

小蛇学python（14）K-means预测花朵种类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from keras.models import Sequential #序列串行类
from keras.layers import Dense #密集层（全连接神经网络）
from keras.wrappers.scikit_learn import KerasClassifier #与sklearn的包装接口
from keras.utils import np_utils #
from sklearn.model_selection import cross_val_score # 交叉验证准确度得分
from sklearn.model_selection import KFold # k折交叉验证
from sklearn.preprocessing import LabelEncoder # 标签编码（转化为数值，类似向量化）
from keras.models import model_from_json # 训练模型的储存

# reproducibility
seed = 13 # 伪随机数种子
np.random.seed(seed)

# load data
df = pd.read_csv('iris.csv')
# from sklearn.datasets import load_iris
# df = load_iris()
X = df.values[:,0:4].astype(float) #设定为单精度浮点类型
Y = df.values[:,4]

encoder = LabelEncoder() #新建编码器
Y_encoded = encoder.fit_transform(Y) #进行数值转换
Y_onehot = np_utils.to_categorical(Y_encoded) #转化为向量

#define a network
def baseline_model():
	model = Sequential()
	model.add(Dense(7, input_dim=4, activation='tanh')) #新建(隐藏)层：Dense全连接，7个神经元，输入维度为4，激活函数为tanh双曲正切
	model.add(Dense(3, activation='softmax')) #新建输出层，3个输出，激活函数为softmax
	model.compile(loss='mean_squared_error', optimizer='sgd', metrics=['accuracy']) #损失函数：最小均方。优化方法：随机梯度下降。评估指标：准确度
	return model

estimator = KerasClassifier(build_fn=baseline_model, epochs=20, batch_size=1, verbose=1)
# 交叉验证。 build_fn：模型生成方法。epochs：训练次数。batchsize：批处理容量。verbose：输出信息详细度。
# epchs如果增加到200，准确率可达97%。

#evalute
kfold = KFold(n_splits=10, shuffle=True, random_state=seed)
# n_split：将数据集分成10份。shuffle：乱序预处理。
result = cross_val_score(estimator, X, Y_onehot, cv=kfold)
print("Accuray of cross validation, mean %.2f,std %.2f" % (result.mean(), result.std())) #均值、方差

#save model
estimator.fit(X, Y_onehot)
model_json = estimator.model.to_json()
with open("model.json", "w") as json_file:  # 保存结构
	json_file.write(model_json)

estimator.model.save_weights("model.h5") # 保存数值
print("save model to disk")

# load model and use it for prediction
json_file = open("model.json", "r")
loaded_model_json = json_file.read()
json_file.close()
loaded_model = model_from_json(loaded_model_json)
loaded_model.load_weights("model.h5")
print("loaded model from dish")

predicted = loaded_model.predict(X)
print("predicted probability:" + str(predicted))

predicted_label = loaded_model.predict_classes(X)
print("predicted label:" + str(predicted_label))

一些知识

softmax函数：

softmax存在数值问题。（中间有指数膨胀）

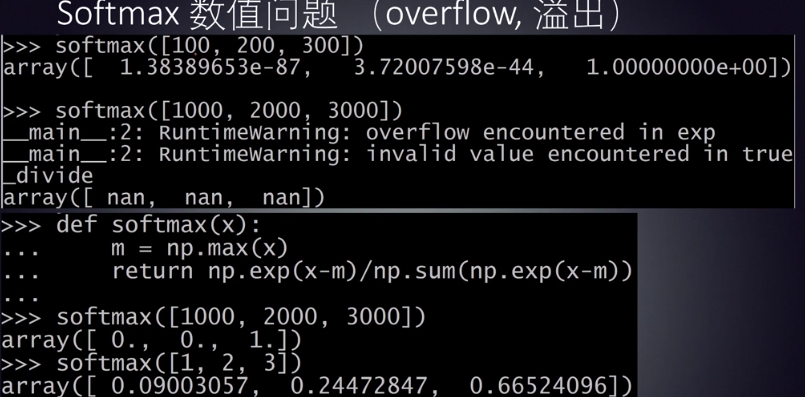
可以利用最大值偏置进行修正。避免溢出。

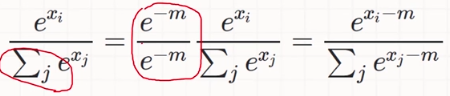
tanh函数：

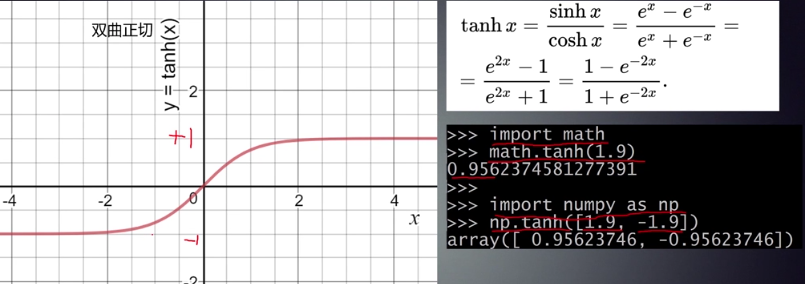
深度神经网络

深度神经网络的两大挑战：

  • 梯度消亡（Gradient Vanishing）：训练过程非常慢。

  • 过拟合（Overfitting）：在训练数据上效果好，在测试数据集上效果差。

梯度消亡

神经网络靠近输入端的网络层系数变化不敏感。当网络层数增加时，现象更明显。

梯度消亡的前提：

  • 使用基于梯度的训练方法
  • 激活函数的输出值范围远小于输入值范围（sigmoid、tanh、softmax）

实际上，对于这样的激活函数，100、10000和10005三者的激活值几乎一致。

如果一个（大）系数的微小变化对网络的影响很小，那么就很难进行优化（优化特别慢）。训练起来就很困难了。

可以想象的是，损失函数是一个非常平坦的凹面。

ReLU激活

  • ReLU:$f(x)=max(0,x)$。
    • 正值梯度。
  • LeakyReLU:$f(x)=max(ax,x)$。
    • 优化了负值梯度。

为什么不直接选择激活函数$f(x)=x$（恒同映射）？

激活函数一定要是非线性的。如果激活函数是线性函数，那么最后得到的就是一个线性分类器。
激活函数的非线性越强，那么分类能力也就越强。

非梯度训练方法

过拟合

解决方案：

  • Dropout
  • L2正则化
  • L1正则化
  • MaxNorm

Dropout

Dropout: A Simple Way to Prevent Neural Networks from Overfitting

【论文精读】Dropout: A Simple Way to Prevent Neural Networks from …，Atlas8346

Dropout可以被解释为一种通过在隐藏的单元中添加噪声来调节神经网络的方法。

大概意思就是引入神经元的休息状态。神经元有一定概率被Dropout，也就完全不能被激活，从而输出全为0。

L2正则化

L1正则化

MaxNorm

神经网络系数的初始化

实战项目1: 自动为图片生成描述 Image Captioning

环境安装参考：机器学习初等指南(1)-环境安装与使用

Task1 构建VGG16

经典的网络有：VGG, ResNet, DenseNet。

深度学习卷积神经网络——经典网络VGG-16网络的搭建与实现 …

VGGNet探索了卷积神经网络的深度与其性能之间的关系，通过反复堆叠3 3的小型卷积核和2 2的最大池化层，VGGNet成功地构筑了16~19层深的卷积神经网络。VGGNet相比之前state-of-the-art的网络结构，错误率大幅下降， VGGNet论文中全部使用了3 3的小型卷积核和2 2的最大池化核，通过不断加深网络结构来提升性能。

一文读懂VGG网络- 知乎

简单来说，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5x5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。

VGG16学习笔记| 韩鼎の个人网站，https://github.com/handsomeboy/vgg16

Kaggle-VGG16

Pre-卷积

万字长文带你看尽深度学习中的各种卷积网络（上篇）

万字长文带你看尽深度学习中的各种卷积网络（下篇）

A Comprehensive Introduction to Different Types of Convolutions in Deep Learning

如何通俗易懂地解释卷积？

如何理解 Graph Convolutional Network（GCN）？

深度学习笔记5：池化层的实现 max-pooling和mean-pooling

卷积层与池化层 卷积向下取整，池化向上取整。

例题：（Here）

  • 输入图片大小为200×200，依次经过一层卷积（kernel size 5×5，padding 1，stride 2），pooling（kernel size 3×3，padding 0，stride 1），又一层卷积（kernel size 3×3，padding 1，stride 1）之后，输出特征图大小为？

答案：97。

公式：

卷积层1：(input_size - kernel_size + 2*padding)/stride + 1=(200-5+2*1)/2+1 $$\longrightarrow$$floor(99.5)=99

池化层：(99-3)/1+1 $$\longrightarrow$$ceil(97)=97

卷积层2：(97-3+2*1)/1+1 $$\longrightarrow$$floor(97)=97

全连接层的作用是什么？

全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。在实际使用中，全连接层可由卷积操作实现：对前层是全连接的全连接层可以转化为卷积核为1x1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积，h和w分别为前层卷积结果的高和宽。

以VGG-16为例，对224x224x3的输入，最后一层卷积可得输出为7x7x512，如后层是一层含4096个神经元的FC，则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程，其中该卷积核参数如下：

“filter size = 7, padding = 0, stride = 1, D_in = 512, D_out = 4096”

经过此卷积操作后可得输出为1x1x4096。

如需再次叠加一个2048的FC，则可设定参数为“filter size = 1, padding = 0, stride = 1, D_in = 4096, D_out = 2048”的卷积层操作。

目前由于全连接层参数冗余（仅全连接层参数就可占整个网络参数80%左右），近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代FC来融合学到的深度特征，最后仍用softmax等损失函数作为网络目标函数来指导学习过程。需要指出的是，用GAP替代FC的网络通常有较好的预测性能。

微调（fine tuning）是深度学习领域最常用的迁移学习技术。

CNN中卷积层的计算细节

一文读懂卷积神经网络中的1x1卷积核

1x1卷积一般只改变输出通道数（channels），而不改变输出的宽度和高度。

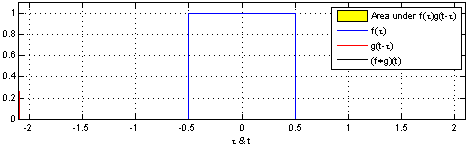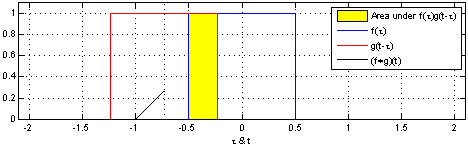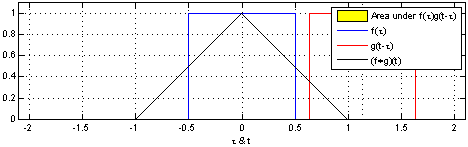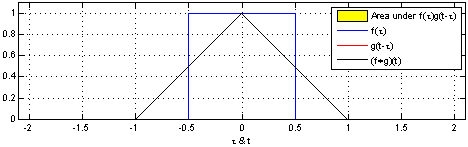
卷积：一个函数经过区间镜像翻转和平移后与另一个函数的乘积的积分。

Source: http://fourier.eng.hmc.edu/e161/lectures/convolution/index.html

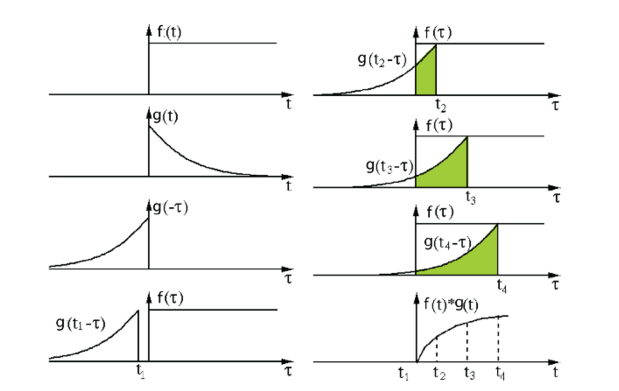
在深度学习中，卷积中的过滤函数是不经过翻转的。

深度卷积：一个函数f经过平移后与另一个函数g的乘积的积分。深度卷积即互关联（Cross-correlation）。

过滤函数：函数 g 称为一个过滤函数。

执行卷积的目的就是从输入中提取有用的特征。

真子空间：一个空间若真包含于另一个空间，那么它就是另一个空间的子空间。

张量空间：一个空间如果是以张量（多维离散立方体）的形式定义的，就叫张量空间。

一张图像就是张量空间（矩阵空间）上的一个点，也就是张量。

窗口：一个真子空间称为原空间的一个窗口。

通道（channel）：如果过滤函数g在张量空间中有一个窗口，在这个窗口外g恒零，那么称这个窗口叫g的通道。

卷积核（kernel）：给定张量空间，一个存在通道的过滤函数g，称为张量空间上的一个卷积核。

卷积核本身就是张量。一般而言，定义卷积核同时就应该明确指定所使用的通道。

在深度学习中，卷积就是元素级别（ element-wise） 的乘法和加法。

对于一张具有单通道（单卷积核）的图像，卷积过程如上图所示，过滤函数是一个组成部分为[[0, 1, 2], [2, 2, 0], [0, 1, 2]]的 3 x 3 矩阵，它滑动穿过整个输入。在每一个位置，它都执行了元素级别的乘法和加法，而每个滑过的位置都得出一个数字，最终的输出就是一个 3 x 3 矩阵。（注意：在这个示例中，卷积步长=1；填充=0。）

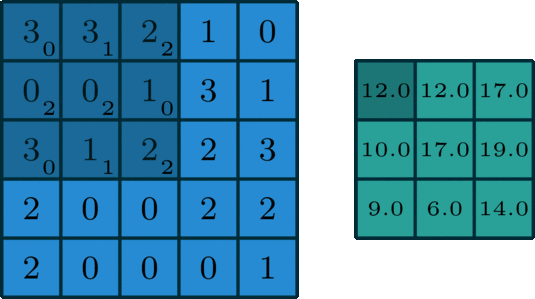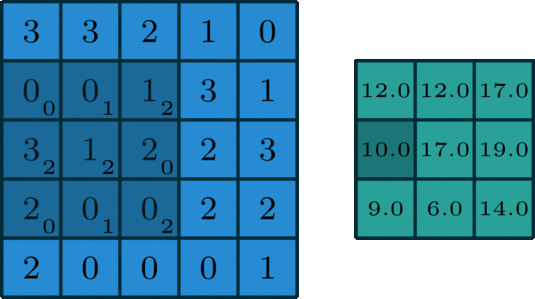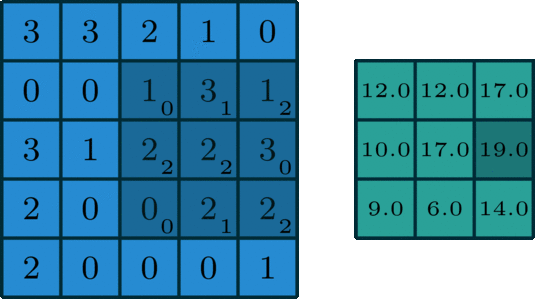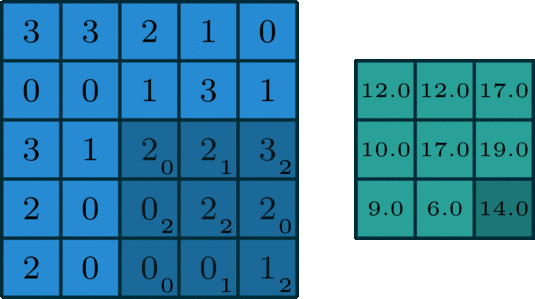
Source: https://en.wikipedia.org/wiki/Convolution

滑动卷积：过滤函数不变，卷积核遍历所有相同规模的窗口，上图所示的过程就是滑动卷积。

如果按照一定步长迭代，并非遍历的话，也可以有类似的讨论。叫做广义滑动卷积。

覆盖卷积：如果张量上定义若干个卷积核，这些卷积核的通道构成张量空间的一个覆盖)，则这些卷积核可覆盖卷积。

滑动卷积是覆盖卷积的特例。

插一句，有限覆盖定理。（虽然没什么关系~）

卷积映射（卷积层）：一个张量被若干卷积核覆盖卷积，获得新张量，则称为卷积映射。

卷积映射函数即过滤器（filter）。有时过滤器也指若干卷积核堆积形成的张量。

一个卷积映射就对应一个卷积层。

通过卷积映射，原张量被嵌入到一个相对规模更小的张量空间中。

卷积核可以不一样哦。不一定等效于滑动卷积了。

卷积核大小（Kernel size）：卷积核的窗口的大小。

卷积步长（Stride）：卷积核滑动通过图像的步长。

填充（Padding）：填充定义如何处理图像的边界。

  • 空填充（将输入边界周围的填充设置为 0，padding='same'）

  • 不填充（映射后张量变小，padding='valid'）

Tensorflow中padding的两种类型SAME和VALID

A guide to convolution arithmetic for deep learning （《深度学习的卷积算法指南》，详细介绍各种卷积核操作）

多通道卷积：如果覆盖卷积中任意一个卷积核都构成滑动卷积，那么称为多通道卷积。

下面是一个3个卷积核的滑动卷积（RGB位图）。一个图像可以是多层的，滑动卷积只需要在某一层上滑动。

Source: https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

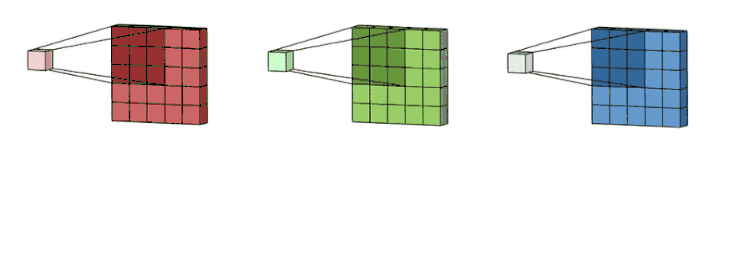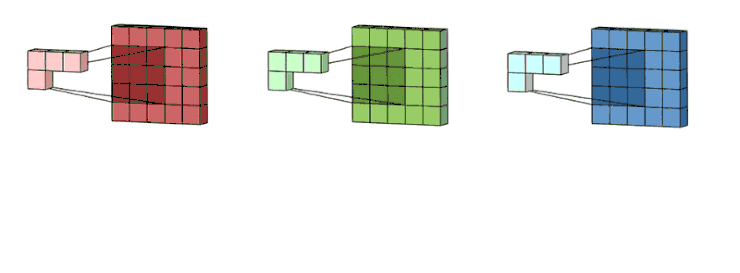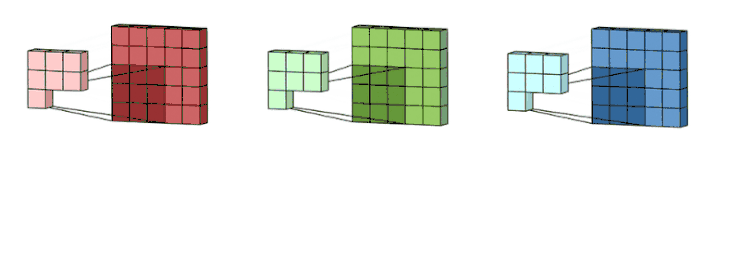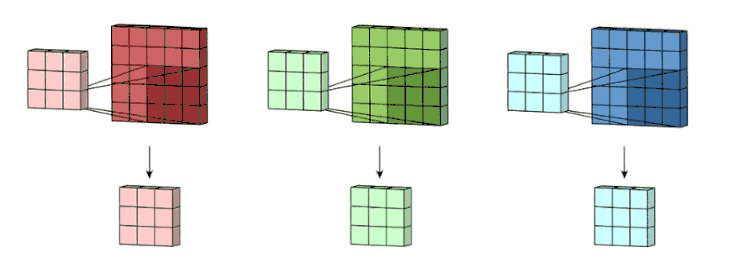
之后，这 3 个通道都合并到一起（元素级别的加法）组成了一个大小为 3 x 3 x 1 的单通道。
这个通道是输入层（5 x 5 x 3 矩阵）使用了过滤器（3 x 3 x 3 矩阵）后得到的结果。

更广义的如下图：（紫色部分的长度就是通道数目，全部合并）

这其实就是高维卷积核（过滤器）。

如果通道不发生合并：（Din=Dout）

img

以及推广的高维卷积核，窗口可以在多个维上滑动：（Din>Dout）

在执行计算昂贵的 3 x 3 卷积和 5 x 5 卷积前，往往会使用 1 x 1 卷积来减少计算量。

1 x 1 卷积最初是在 Network-in-network 的论文中被提出的，之后在谷歌的 Inception 论文中被大量使用。

转置卷积：卷积映射的对应的张量膨胀的卷积称为一个转置卷积。

如果转置卷积映射存在逆映射，则称为逆卷积。

转置卷积的原理如下图所示：

1

2

转置的含义来自上述原理中的矩阵的转置。而逆来自逆映射。

空洞卷积（Dilated Convolution）：在卷积核部分之间插入空间让卷积核膨胀。即扩张卷积。

类似海绵。本质上是在不增加额外的计算成本的情况下增加感受野。

《使用深度卷积网络和全连接 CRF 做语义图像分割》（Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs，https://arxiv.org/abs/1412.7062）

《通过空洞卷积做多规模的上下文聚合》（Multi-scale context aggregation by dilated convolutions，https://arxiv.org/abs/1511.07122）

还有可分离卷积、扁平化卷积、分组卷积等。（详见Here）

VGG引述

VGG是由Simonyan 和Zisserman在文献《Very Deep Convolutional Networks for Large Scale Image Recognition》（PDF）中提出卷积神经网络模型，其名称来源于作者所在的牛津大学视觉几何组(Visual Geometry Group)的缩写。

该模型参加2014年的 ImageNet图像分类与定位挑战赛，取得了优异成绩：

  • 在分类任务上排名第二，在定位任务上排名第一。

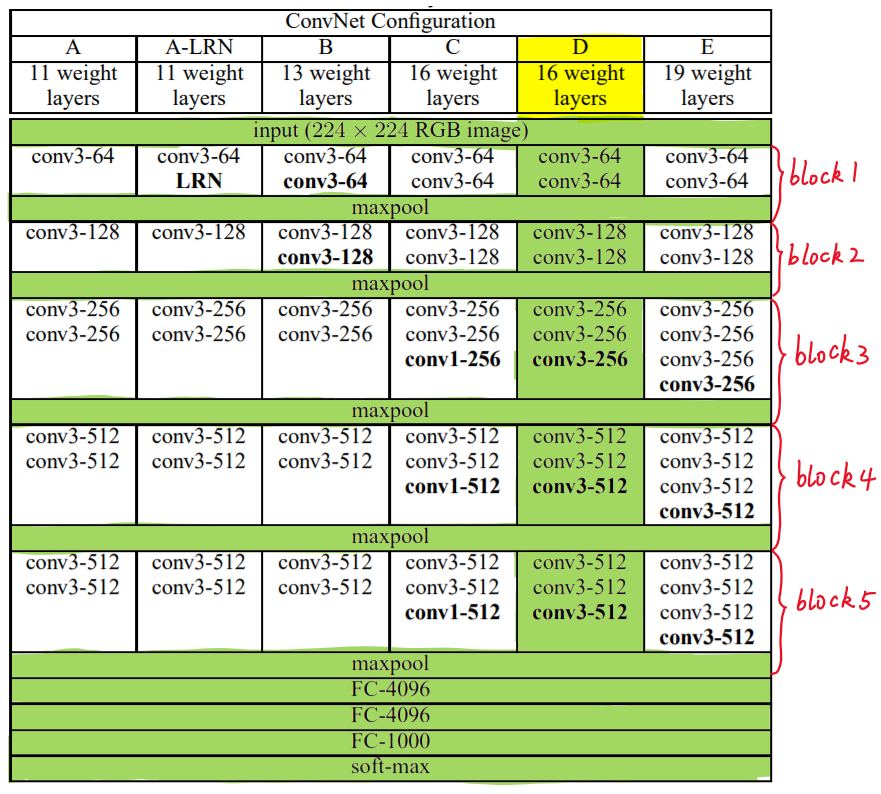
VGG分类

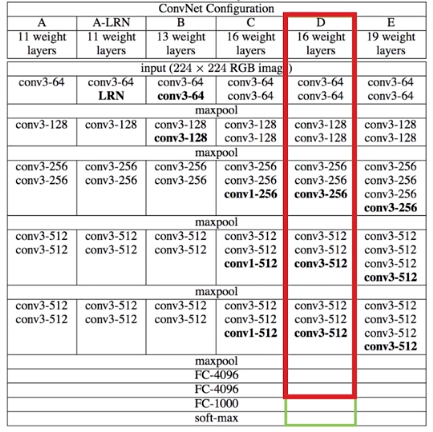
VGG中根据卷积核大小和卷积层数目的不同，可分为A，A-LRN,B,C,D,E共6个配置(ConvNet Configuration)，其中以D,E两种配置较为常用，分别称为VGG16和VGG19。

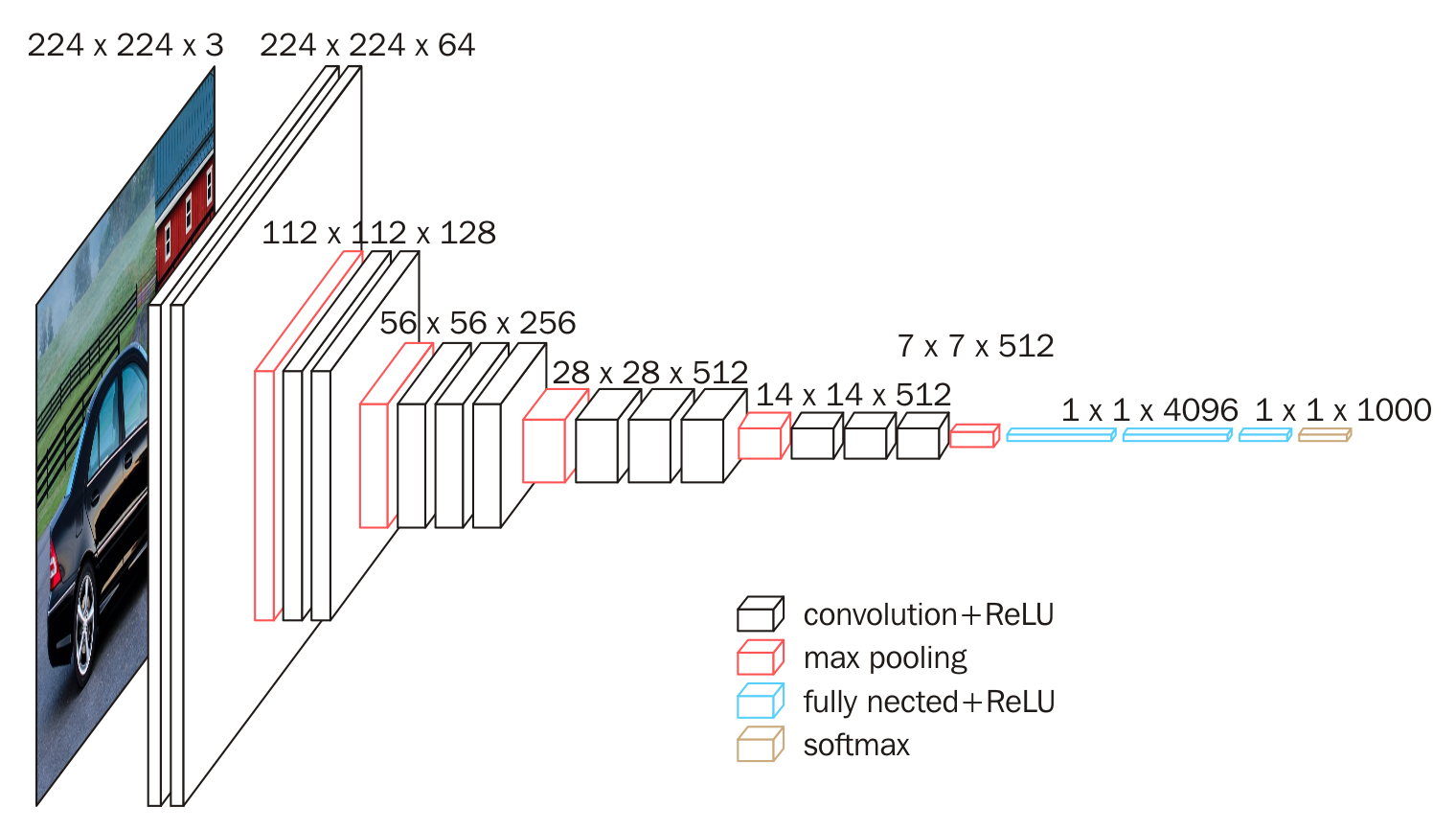
对VGG16进行具体分析发现，VGG16共包含：

  • 13个卷积层（Convolutional Layer），分别用conv3-XXX表示
  • 3个全连接层（Fully connected Layer）,分别用FC-XXXX表示
  • 5个池化层（Pool layer）,分别用maxpool表示

其中，卷积层和全连接层具有权重系数，因此也被称为权重层，总数目为13+3=16，这即是VGG16中16的来源。(池化层不涉及权重，因此不属于权重层，不被计数)。

VGG的优点

VGG16的突出特点是简单，体现在：

  • 卷积层均采用相同的卷积核参数：
    • 卷积层均表示为conv3-XXX，其中conv3说明该卷积层采用的卷积核的尺寸(kernel size)是3，即宽（width）和高（height）均为3，3*3是很小的卷积核尺寸，结合其它参数（步幅stride=1，填充方式padding=same），这样就能够使得每一个卷积层(张量)与前一层（张量）保持相同的宽和高。XXX代表卷积层的通道数。
  • 池化层均采用相同的池化核参数池化层的参数均为2×2，步幅stride=2，max的池化方式，这样就能够使得每一个池化层（张量）的宽和高是前一层（张量）的1/2。
  • 模型是由若干卷积层和池化层堆叠（stack）的方式构成，比较容易形成较深的网络结构（在2014年，16层已经被认为很深了）。

综合上述分析，可以概括VGG的优点为: Small filters, Deeper networks

VGG的缺点

训练时间过长，调参难度大。

存储容量大，不利于部署。（存储VGG16权重值文件的大小为500多MB）

块（Block）

VGG16的卷积层和池化层可以划分为不同的块（Block），从前到后依次编号为Block1~block5。

  • 每一个块内包含若干卷积层和一个池化层。
  • 同一块内，卷积层的通道（channel）数是相同的。
    • block3: 3个卷积层，卷积核尺寸为3*3，通道数都是256

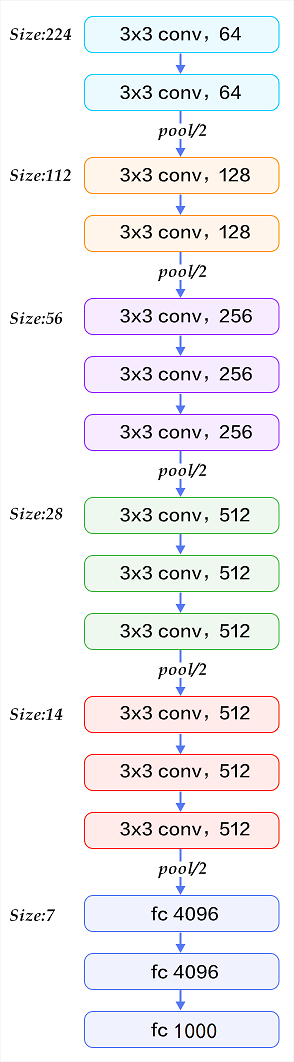
随着层数的增加：

  • 卷积通道数翻倍：64→128→256→512（到512不再增加了）
  • 张量尺寸减半：224→ 112→ 56→28→ 14→ 7（池化层）

VGG参数

VGG参数包括卷积核参数和全连接层参数。两者都需要学习得到。

  • 卷积核参数
    • 对于第一层卷积，由于输入图的通道数是3（RGB），网络必须学习大小为3×3，通道数为3的的卷积核，这样的卷积核有64个，因此总共有（3×3 × 3）× 64 = 1728个参数。
  • 全连接层参数
    • =前一层节点数×本层的节点数。
  • 最大池化层没有参数

FeiFei Li在CS231的课件中给出了整个网络的全部参数（138 357 544 个参数）的计算过程（不考虑偏置），如下图所示，图中红色是计算所需存储容量的部分；蓝色是计算权重参数数量的部分：（Lecture 9: CNN Architectures）

VGG16

VGG16构建代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D
from keras.layers import MaxPooling2D

def generate_vgg16():
    input_shape = (224, 224, 3) # 输入: 224*244，RGB三位图
    model = Sequential([
    	Conv2D(64, (3, 3), input_shape=input_shape, padding='same', activation='relu'),
    	# 卷积层，64个滤波器（卷积核），尺寸3*3，参数：输入规格，填充，激活函数
    	Conv2D(64, (3, 3), padding='same', activation='relu'),
    	# 非首层无需指定输入规格
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),

    	# Block 2
    	Conv2D(128, (3, 3), padding='same', activation='relu'),
    	Conv2D(128, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	
    	# 3
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 4
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 5
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 全连接层
    	Flatten(),
    	Dense(4096, activation='relu'),
    	Dense(4096, activation='relu'),
    	Dense(1000, activation='softmax')
    	# 最后要做一个softmax，输出概率归一化
    	])
    return model

if __name__ == '__main__':
	# 主函数，调用
    model = generate_vgg16()
    model.summary()

输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
Using TensorFlow backend.
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 224, 224, 64)      1792      
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 224, 224, 64)      36928     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 112, 112, 64)      0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 112, 112, 128)     73856     
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 112, 112, 128)     147584    
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 56, 56, 128)       0         
_________________________________________________________________
conv2d_5 (Conv2D)            (None, 56, 56, 256)       295168    
_________________________________________________________________
conv2d_6 (Conv2D)            (None, 56, 56, 256)       590080    
_________________________________________________________________
conv2d_7 (Conv2D)            (None, 56, 56, 256)       590080    
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 28, 28, 256)       0         
_________________________________________________________________
conv2d_8 (Conv2D)            (None, 28, 28, 512)       1180160   
_________________________________________________________________
conv2d_9 (Conv2D)            (None, 28, 28, 512)       2359808   
_________________________________________________________________
conv2d_10 (Conv2D)           (None, 28, 28, 512)       2359808   
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 14, 14, 512)       0         
_________________________________________________________________
conv2d_11 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
conv2d_12 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
conv2d_13 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 7, 7, 512)         0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 25088)             0         
_________________________________________________________________
dense_1 (Dense)              (None, 4096)              102764544 
_________________________________________________________________
dense_2 (Dense)              (None, 4096)              16781312  
_________________________________________________________________
dense_3 (Dense)              (None, 1000)              4097000   
=================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0

可以看到参数是138,357,544个，基本可以认为构建无误。

VGG19构建代码

不妨再模拟一个常用的VGG19。

VGG19只是在第3、4、5块（Block）各增加一个卷积层。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from keras.models import Sequential
from keras.layers import Dense, Flatten
from keras.layers import Conv2D
from keras.layers import MaxPooling2D

def generate_vgg16():
    input_shape = (224, 224, 3) # 输入: 224*244，RGB三位图
    model = Sequential([
    	Conv2D(64, (3, 3), input_shape=input_shape, padding='same', activation='relu'),
    	# 卷积层，64个滤波器（卷积核），尺寸3*3，参数：输入规格，填充，激活函数
    	Conv2D(64, (3, 3), padding='same', activation='relu'),
    	# 非首层无需指定输入规格
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),

    	# 2
    	Conv2D(128, (3, 3), padding='same', activation='relu'),
    	Conv2D(128, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	
    	# 3
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	Conv2D(256, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 4
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 5
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	Conv2D(512, (3, 3), padding='same', activation='relu'),
    	MaxPooling2D(pool_size=(2, 2), strides=(2, 2)),
    	# 全连接层
    	Flatten(),
    	Dense(4096, activation='relu'),
    	Dense(4096, activation='relu'),
    	Dense(1000, activation='softmax')
    	# 最后要做一个softmax，输出概率归一化
    	])
    return model

if __name__ == '__main__':
	# 主函数，调用
    model = generate_vgg16()
    model.summary()

输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
Using TensorFlow backend.
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 224, 224, 64)      1792      
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 224, 224, 64)      36928     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 112, 112, 64)      0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 112, 112, 128)     73856     
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 112, 112, 128)     147584    
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 56, 56, 128)       0         
_________________________________________________________________
conv2d_5 (Conv2D)            (None, 56, 56, 256)       295168    
_________________________________________________________________
conv2d_6 (Conv2D)            (None, 56, 56, 256)       590080    
_________________________________________________________________
conv2d_7 (Conv2D)            (None, 56, 56, 256)       590080    
_________________________________________________________________
conv2d_8 (Conv2D)            (None, 56, 56, 256)       590080    
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 28, 28, 256)       0         
_________________________________________________________________
conv2d_9 (Conv2D)            (None, 28, 28, 512)       1180160   
_________________________________________________________________
conv2d_10 (Conv2D)           (None, 28, 28, 512)       2359808   
_________________________________________________________________
conv2d_11 (Conv2D)           (None, 28, 28, 512)       2359808   
_________________________________________________________________
conv2d_12 (Conv2D)           (None, 28, 28, 512)       2359808   
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 14, 14, 512)       0         
_________________________________________________________________
conv2d_13 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
conv2d_14 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
conv2d_15 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
conv2d_16 (Conv2D)           (None, 14, 14, 512)       2359808   
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 7, 7, 512)         0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 25088)             0         
_________________________________________________________________
dense_1 (Dense)              (None, 4096)              102764544 
_________________________________________________________________
dense_2 (Dense)              (None, 4096)              16781312  
_________________________________________________________________
dense_3 (Dense)              (None, 1000)              4097000   
=================================================================
Total params: 143,667,240
Trainable params: 143,667,240
Non-trainable params: 0

QA

  1. 提交作业时，所有文件都需要上传吗？还是只需要上传修改后的.py文件？

    未回答。（Remain）

    是的。

  2. 代码中卷积核只指定了窗口的大小3*3，那么卷积核的过滤函数是怎么确定的呢？

    参数通过通过反向传播训练的。Check！

  3. 图像是RGB三位（层）的，为什么不是指定3个卷积核形成过滤器（滑动窗口），而是64、128……？步长是keras自行确定的吗？指定的卷积核个数是在图像上默认均匀分布吗？而且64个3*3窗口根本没法覆盖224x224的图像啊。。orz

    64代表卷积核的个数，步长自己设，keras默认步长应该是1。卷积通过滑动覆盖整个图片。

    RGB只有3个通道，64个卷积核不应该对应64个通道吗，怎么滑动？

    64个卷积核是指单个图像被64个过滤器分别过滤了。64通道是处理后的通道，224 224 3处理后可以变成224 224 64。

    “处理”具体对应的是哪一步？什么操作？

    处理代表卷积层；通过卷积层之后通道数就变了。

  4. Conv2D的filters和strides参数不会互相冲突吗？它们指定的对象有什么区别？

    filters代表卷积核个数，stride代表步长，没有冲突。Check！

  5. 多个卷积层堆积到一起究竟有多大意义？我看padding都是从输入图像最边缘的一层像素开始的，就算迭代3次，外部的padding也只能向内传播3个像素深度，除了增加算力以外有什么好处吗？我难道不可以直接设置一个具有新的过滤[复合函数]的卷积核来完成这样的工作吗？

    多个卷积核，每个卷积核的参数都是不一样的，相当于你说的复合函数。

    有什么好处？如果相当于复合函数为什么不直接用复合函数？

    是因为神经网络其实本身就是通过不断训练，梯度下降，达到某一个复杂函数的效果。（Remain）

    （深层次）训练效果更好。

  6. 我看VGG模型的C配置里有conv1-512，能讲讲1 1卷积核的作用吗？这里的图像也就三层，为什么要反复用1 1卷积呢？类似于一个像素级的激活函数吗？（那么还要ReLU干啥呢。。）另外1 1为什么要放在33卷积核的[后面]？

    1 * 1卷积核用于改变通道个数，比如从12 12 256变成12 12 512就可以用1 * 1卷积层。

    那不同配置卷积层数不同不影响通道吗？Check！

  7. 池化层到底干了个啥？为啥每次池化了以后通道数翻倍呢？

    池化层用于下采样。通道变多是为了组合不同的特征。

    我想问的是通道为什么会变多？（不是问“为了什么而变多”orrrrz）

    因为卷积核个数多了，处理代表卷积层；通过卷积层之后通道数就变了。

    卷积可以改变通道数？？？池化也可以改变通道数？Check！

    我还是不太理解卷积核数大于通道数是如何过滤的？神奇的操作？？

    嗯嗯，一个卷积核就可以把之前的所有通道都进行一遍卷积操作，输出为n m 1，x个卷积层就是n m x，所以x跟之前的层有多少通道没关系。

Task2 特征提取

迁移学习

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
from keras.models import model_from_json
from PIL import Image as pil_image
from keras import backend as K
import numpy as np
from pickle import dump
from os import listdir
import os
from keras.models import Model
import keras
from tqdm import tqdm

def load_img_as_np_array(path, target_size):
    """从给定文件[加载]图像,[缩放]图像大小为给定target_size,返回[Keras支持]的浮点数numpy数组.

    # Arguments
        path: 图像文件路径
        target_size: 元组(图像高度, 图像宽度).

    # Returns
        numpy 数组.
    """
    img = pil_image.open(path) # 打开文件
    img = img.resize(target_size,pil_image.NEAREST) # NEARSET 是一种插值方法
    return np.asarray(img, dtype=K.floatx()) #转化为向量


def preprocess_input(x):
    """预处理图像用于网络输入, 将图像由RGB格式转为BGR格式.
       将图像的每一个图像通道减去其均值
       均值BGR三个通道的均值分别为 103.939, 116.779, 123.68

    # Arguments
        x: numpy 数组, 4维.
        data_format: Data format of the image array.

    # Returns
        Preprocessed Numpy array.
    """
    # 'RGB'->'BGR', https://www.scivision.co/numpy-image-bgr-to-rgb/
    x = x[..., ::-1]
    mean = [103.939, 116.779, 123.68]

    x[..., 0] -= mean[0]
    x[..., 1] -= mean[1]
    x[..., 2] -= mean[2]

    return x

def load_vgg16_model():
    """从当前目录下面的 vgg16_exported.json 和 vgg16_exported.h5 两个文件中导入 VGG16 网络并返回创建的网络模型
       vgg16_exported.json 下载链接：链接: https://pan.baidu.com/s/13WQBRb4sr3umP7xbUCxmCg 提取码: ycb5 
       vgg16_exported.h5 下载链接: https://pan.baidu.com/s/1yF8wybHuzGoTzwSkqTPzzQ 提取码: ub75
       注意上传完成的作业时不要上传这两个文件
    # Returns
        创建的网络模型 model
    """
    json_file = open("vgg16_exported.json","r")
    loaded_model_json = json_file.read()
    json_file.close()

    model = model_from_json(loaded_model_json)
    model.load_weights("vgg16_exported.h5")

    return model

def extract_features(directory):
    """提取给定文件夹中所有图像的特征, 将提取的特征保存在文件features.pkl中,
       提取的特征保存在一个dict中, key为文件名(不带.jpg后缀), value为特征值[np.array]

    Args:
        directory: 包含jpg文件的文件夹

    Returns:
        None
    """
    model = load_vgg16_model()
    # 去除模型最后一层
    model.layers.pop()
    model = Model(inputs=model.inputs, outputs=model.layers[-1].output)
    print("Extracting...")

    features = dict()
    pbar = tqdm(total=len(listdir(directory)), desc="进度", ncols=100)
    for fn in listdir(directory):
        print("\tRead file:", fn)
        fn_path = directory + '/' + fn

        # 返回长、宽、通道的三维张量
        arr = load_img_as_np_array(fn_path, target_size=(224,224))

        # 改变数组的形态，增加一个维度（批处理）—— 4维
        arr = arr.reshape((1, arr.shape[0], arr.shape[1], arr.shape[2]))
        # 预处理图像为VGG模型的输入
        arr = preprocess_input(arr)
        # 计算特征
        feature = model.predict(arr, verbose=0)

        print("\tprocessed...",end='')
        id = os.path.splitext(fn)[0]
        features[id] = feature
        print("Saved. ", id)
        pbar.update(1)

    print("Complete extracting.")
    return features

if __name__ == '__main__':
    # 提取Flicker8k数据集中所有图像的特征，保存在一个文件中, 大约一小时的时间，最后的文件大小为127M
    # Flickr8k数据集的下载链接: https://pan.baidu.com/s/1bQcQAz0pxPix9q9kCoZ1aw 提取码: 6gpd 
    # 下载zip文件，解压缩到当前目录的子文件夹Flicker8k_Dataset， 注意上传完成的作业时不要上传这个数据集文件
    directory = './Flicker8k_Dataset'
    features = extract_features(directory)
    print('提取特征的文件个数：%d' % len(features))
    print(keras.backend.image_data_format())
    #保存特征到文件
    dump(features, open('features.pkl', 'wb'))

Task3 数据生成

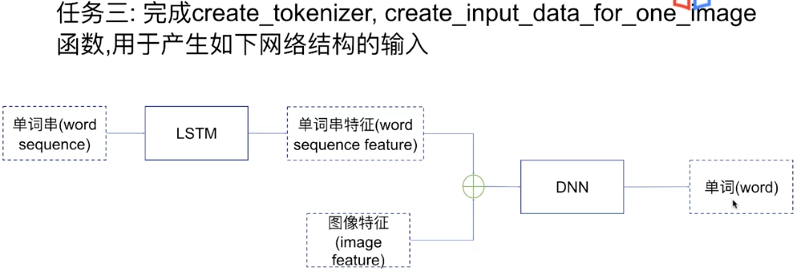
代码

1

Task4 训练网络

代码

1

Task5 模型评估

代码

1

实战项目2：自动驾驶之交通牌识别

实战项目3： （开放式）自动驾驶之方向盘操纵