本文为《 赛博智能经济与区块链》的公众号文章撰写任务。
References
How to Explain Zero-Knowledge Protocols to Your Children
引子
什么是零知识证明?
零知识证明看上去字面上好像是“不用任何知识就证明了某件事情”的意思。。但是事情并非如此简单……
首先我们一定明白,零知识证明不可能等于没有利用任何信息而完成证明。如果有人宣称他证明了哥德巴赫猜想,那么他也至少需要给各位发送这样一条“声明”:“兄弟们,快来看看!新鲜的哥德巴赫猜想证明。俺完成的。”这本身就是一种信息的传递。
事实上大家也注意到,证明是一个信息交互的过程。
那么,我们不由得疑惑:
零知识证明,究竟“零知识”到什么程度?
我们可以把缜密的逻辑推理看作是强证明。因为没有什么比详细的证明步骤更有说服力了。
但是,想像一下,现实生活里面,如果不通过缜密的逻辑推理(To be fair,不是所有人都适合这个方式),我们平时是怎么作证明?
古人云:“论迹不论心。”假如我们没有条件以理服人,那么用行动证明自己也是不错的选择。
和缜密逻辑所代表的非交互式证明不同,行动代表了一类交互式证明的模式。
三色问题
看来我们可以尝试认为足够数量的行为可以揭露事物背后隐藏的真实。所谓实践是检验真理的唯一标准。
想像我们要进行一项三种颜色的涂色问题(三色问题),同样保证相邻不同色:
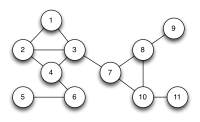
一种可能的解决方案如下:
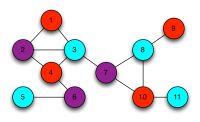
三色问题实际上是一个NP完全问题,这意味着为了寻找一个有效的解,将花费巨额的时间成本。如果提问者给出了一个三色问题,回答者找到了相应的解,他肯定倾向于在得到报酬之前对解进行保密。那么,回答者要怎么证明他获得了这个解,并且不透露其它的任何多余信息呢?
首先我们把得到的解决方案上的涂色全部掩盖住:
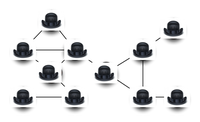
提问者每次可以揭示一组相邻节点的涂色,验证是否满足不同色条件:
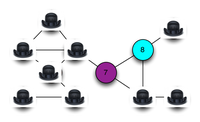
为了揭示时不透露方案真正的涂色,这里应该引入一种随机化的动态映射,每次揭示前,将图中的颜色按随机生成的置换群映射成另外的某种颜色。这样,尽管提问者知道解的性质,但无法推测出具体的解。
这样的揭示次数足够多,那么回答者拥有正确解的概率就会急剧增加。
当这个概率足够大以后,提问者将可以信任回答者——他确实找到了一个合法的涂色方案。
尽管三色问题只是一个案例,但是作为一个NP完全问题,任何其他的NP问题都可以转化为三色问题的实例。
零知识
Goldwasser, Micali 和 Rackoff 提出三个零知识证明的特性,任何零知识都必须满足。简单来说:
- 完整性(Completeness)。如果证明方和验证方都是诚实的,并遵循证明过程的每一步,进行正确的计算,那么这个证明一定是成功的,验证方一定能够接受证明方。
- 安全性(Soundness)。没有人能够假冒证明方,使这个证明成功。
- 零知识性(Zero-knowledgeness)。证明过程执行完之后,验证方只获得了“证明方拥有这个知识”这条信息,而没有获得关于这个知识本身的任何一点信息。
零知识,指的就是具有第三条特性的信息。其实,这个术语更适合称之为零额外知识。
如果这个信息还同时具有完整、安全性,则称之为零知识证明。
零知识,本质上是对解的一无所知。
这种一无所知表现在:尽管你获得了零知识,但是你求解这个问题的难度不变,你想要获得问题的解的期望计算量不变。
你看到了梦中的海市蜃楼,但却无人指出通向彼岸的路。
图灵测试
你甚至可以把三色问题的一连串揭示看成该领域内的“图灵测试”。
通过足够的测试,那么一个黑箱模型可以被认为具有人类智能;通过足够多的揭示,那么一个黑箱涂色方案可以被认为是给定三色问题的解。
但是,我们知道,在图灵测试中你再怎么测试黑箱是否具有人类智能,也无法从中得知任何构造这样一个具有人类智能的机器的信息——如果可以得到的话,那么人们早就造出强人工智能了。因为用一个真人也是可以在黑箱中假装一个人工智能的。
这意味着图灵测试本身只能提供一个可信的判断,但是黑箱内部的机制究竟是什么样的?
事实是,你完全可以伪造。
时光倒流
想像我们有一台时光机。这台时光机允许你每次测试失败后,回到过去一段时间,针对每一个特定的测试设计一个伪造的信息,从而重新通过该测试。
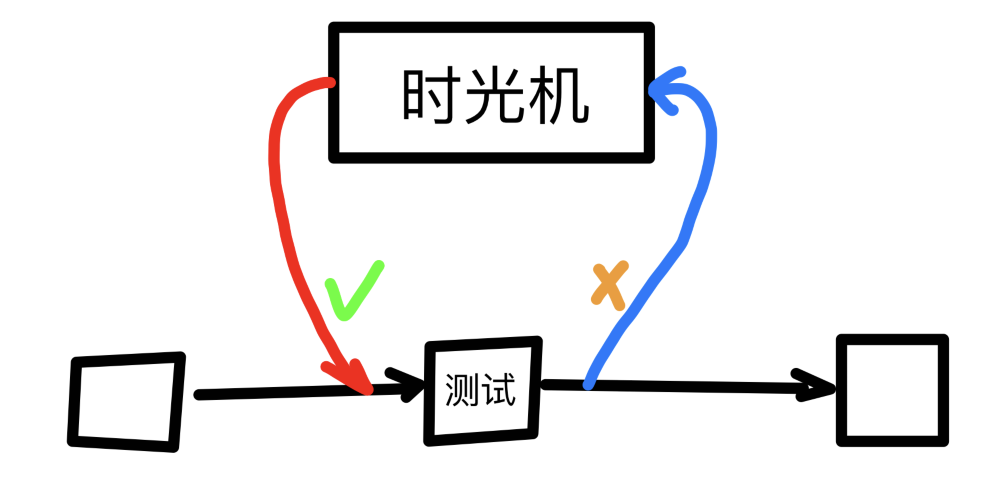
这意味着一个伪造者可以在不知道任何解的信息的情况下,通过所有的测试。其代价无非是在他自己的时间线多花一点时间而已。
看到这里你可能会想:时光机这东西真的存在吗?你说了这么多有什么实际意义?
事实上,时间只不过是一种虚拟的概念,时间的本质是一种有序的链。(是不是想到了区块链?)
在计算机的程序运行过程中,“时光倒流”是司空见惯的,程序回滚、回退并不是遥不可及的手段。比如,某大型程序员线上交友网站所使用的git快照管理技术,就是典型支持时间意义上的版本管理的工具。
任何的验证者计算机(Verifier)程序都可以构造一棵如下图所示的伪造者决策树:
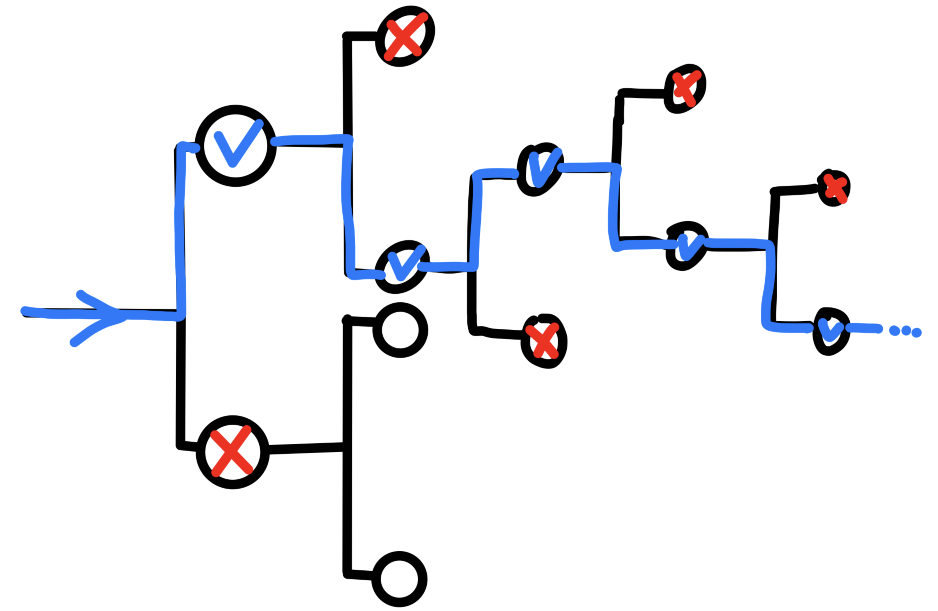
每一次测试都是一个分支点,只需要在分支点处进行有限次的回滚,就一定能够通过测试。
既然一个对解一无所知的伪造者都能通过测试,那么提问者想要从测试中获得关于解的有用信息,看上去就不太可能了……在这种情况下,这样的测试就完成了零知识级的信息传递。
永不坍缩的观测
时光机作弊的特点在于,无论观察多少次,提问者永远无法区分一个有解和另一个对解一无所知的人的区别。
想想,时光倒流,你可以预知你的一切已有经历,但是除此之外你仍然一无所知,从前你不知道的东西现在你依然不知道。
这和量子效应正好相反:只要观测,立刻坍缩。
时光机作弊,达成了永不坍缩的观测。
零知识证明
如果我们要完成一个证明,如果不能区分到底有没有解,那么证明就没有意义了。所以,要形成零知识证明,除了给出了一个满足零知识性的交互方法以外,我们还需要加上一些其它的约束。
即,把时光倒流这种超能力ban掉。
如果限制了时光倒流,强迫整个证明过程在线完成,那么便形成了真正的零知识证明。
但是,交互式的证明是一对一的,在一个区块链里面,发交易的人要向所有矿工证明交易是合法的,双方需要实时交互,交流信息。一个一个证明效率太低太低了。
我们还可以看到,要实现零知识,一个解必须要存在一种与解的结构无关的特征,这种特征是解空间内其它元素所不具有的。我们在测试中,实际测试的就是黑箱是否具有这些特征。
因此,零知识证明协议经历了一段长时期的发展,直到它可以真正被应用到实际工程中去。零知识证明协议变成了一个大家族,这些协议之间具有不同的特点,它们所采用的底层密码学技术也有极大差别。
| 协议特点 | ||
|---|---|---|
| 通用性 | 全能型 | 专用型 (只能证明某些特定的事) |
| 交互性 | 非交互式 | 交互式 |
| 证明规模 | $O(1)$ | $O(n)$ |
为了获得非交互式的证明,计算机科学家尝试把原始问题映射到NP问题。NP问题天然存在验证、求解两个子问题,验证通常十分简单,而求解通常十分繁琐。对于验证者来说,消耗自然很小;对于掌握秘密的人,求解NP问题只需要将秘密映射到相应的NP问题空间;而对于没有掌握秘密的人来说,绕过原始问题直接暴力求解NP问题,是计算上不可行的。
当然,为了保证非交互证明的公平性,通常系统会给出一个公共中立的随机序列(第三方),在证明时加入随机因子。我们考虑“两人分粥”问题,一种常用的公平策略是 Cut and Choose,即一个人分粥,另一个人选粥。这样便避免了证明者自身的偏好。但是,还有一种方法是,引入一个随机选择器,在一个人分粥完成以后,两个人随机地获取其中一份——这样在统计意义上便实现了公平。只不过,这需要一个可信、中立的第三方。
你可以认为非交互式证明是把交互过程打包给了第三方。
2010年,Groth实现了基于椭圆曲线双线性映射的首个全能、非交互、常数大小的零知识证明协议;基于此又发展出了SNARKs协议,并经过不断优化后最终被应用到Zcash数字货币中。Zcash 使用的 NP 问题是 QAP(Quadratic Arithmetic Program),Zcash亦引入了可信的第三方。
对于Zcash数字货币的转账交易而来,零知识证明只需要证明三件事:
- 发送的钱属于发送交易的人
- 发送者发送的金额等于接收者收到金额
- 发送者的钱确实被销毁了
整个过程中矿工并不关心具体花了多少钱,以及参与交易的双方是谁;矿工只关心整个系统的货币是否守恒。
延伸思考1-零知识证明的隐藏前提
零知识的正式内容介绍已经结束了。这一部分的正确性无法保证,只是一种简单的思考。
我的观点是,零知识证明需要一个问题是离线可解的。也就是在获得的相关信息不变的约束下,某个问题单纯通过计算就可以获得解答。
在幻想学中这对应着想界不变。
如果一个问题是想界内不可解的,那么它无法变成一个零知识证明。
如果一个问题,是无法单纯通过计算就可以获得解答,那么在不给出新的信息时,就无法构造出零知识证明。
从另一个角度,零知识证明的前提,应该是对于验证者来说:
- 问题的解是藏在他已知的一个解空间之中的(可知性)
- 对于任意一个解空间中的位置,都可以进行离线的验证(可解性)
也就是说,不是所有的问题和场景都可以构造零知识证明。
延伸思考2-模拟器/时光机佯谬
以下是对证明模拟器/时光机零知识的一个反驳。
虽然我无法区分究竟是在哪个世界、哪个角色,或者有没有使用时光机作弊。
但是,simulator的确从真实世界获得了所有的必要的交互验证信息。
也就是说,如果simulator可以一直保持这样的超能力——那么无论simulator知不知道证明,它对我来说都具有有效的证明力。
也就是,当模拟器具有证明力的时候,它必须与真实世界有连接。一旦它失去连接,它就失去了证明力。也就是说,模拟器相当于真实世界的一个接口 / Interface(它们是一体的不可分的)。模拟器不知道,但是模拟器和真实世界的联合体是知道证明的。
说模拟器不知道证明,就好像在说,我的手不知道我脑袋的想法一样。
就算对于真实世界来说,也不是真实角色的所有的“部分”都拥有零知识证明的信息。
也就是这样的证明方法是不足的。
应该用多重宇宙的方法,在无穷多的平行空间中,存在一个随机宇宙,它不能作弊,但是它也能做出跟真实世界一样的证明。这时,双方就没有连接了。