问题描述

12球问题：12个乒乓球，有一个次品，不知轻重，用一台无砝码天平称三次，找出次品，同时告知轻重？

一种基本解法

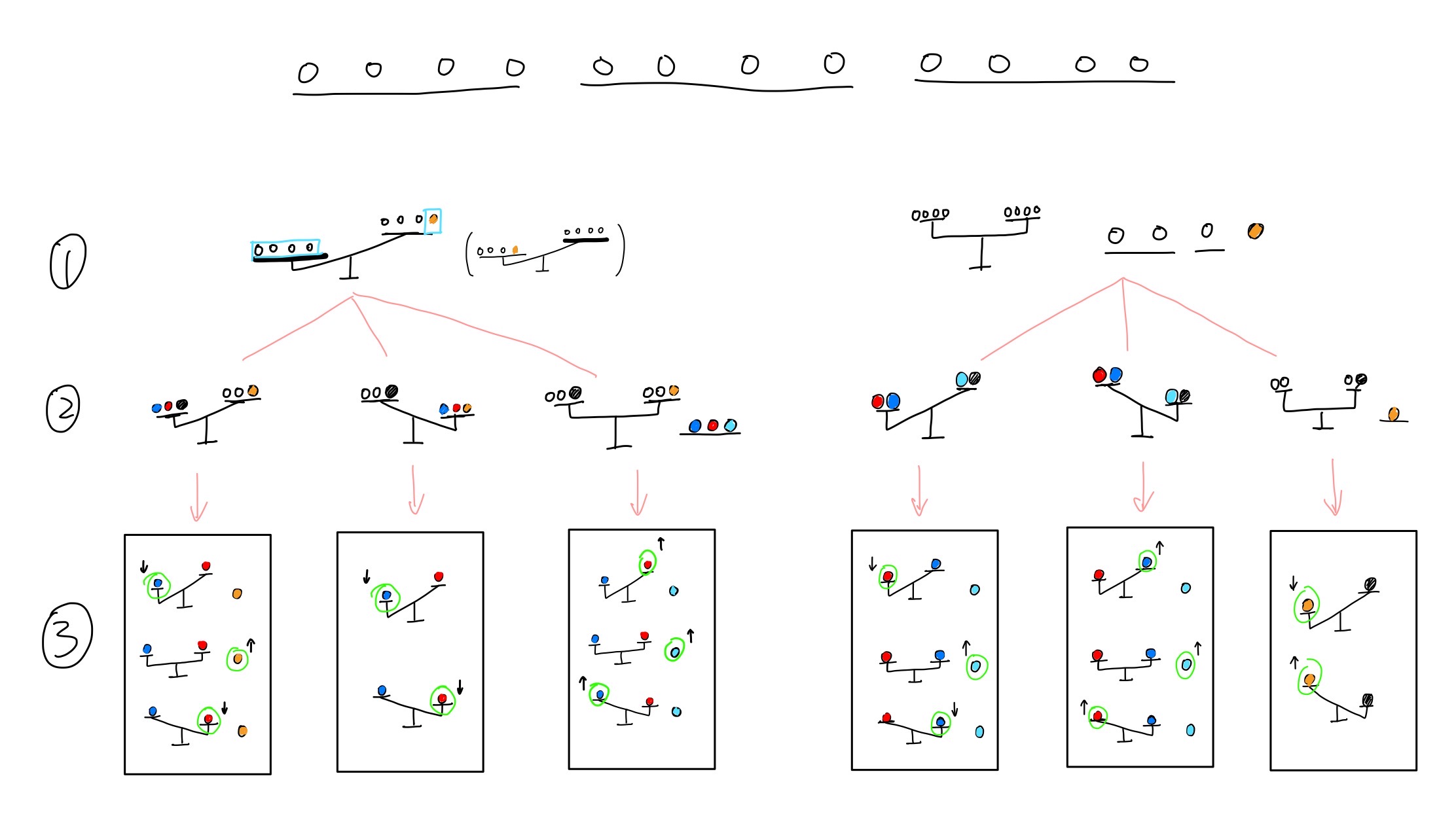
12球问题可以用信息论来保证有解。整个解空间为24，由于天平每次可以三分，所以 12 球问题相对于天平的信息量为 $\log_3 24 <\log_3 27=3$，因此在 3 步内有解。

同时，必须保证第三步时，剩下的解空间 $\leq$ 3。

推论：若有 1 个辅助球，则对于任意含次品的 4 组球（每组相同数量）可以通过 2 次称重，确定次品的轻重和组号。（辅助球，即一个已知的不是次品的标准球）

设组号为 [1, 2, 3, 4]，辅助球为 F

第 1 次测量：分为 3 + 1两份，称完之后解空间分别为3 + 1*2，均 <= 3，信息论可解。

A=[1, 2] vs. B=[3, F]

第 2 次测量：

A = B

C=[4] vs. D=[F]

A < B || A > B

C=[1] vs. D=[2]

13 球问题

对于 13 球问题，可以证明，必须添加一个标准的辅助球才有解。

首先信息量为 $\log_3 26 <\log_3 27=3$，因此理论可解。

引理1：$n$ 个球取 $m$ 个称 1 次后的两种情况的剩余解空间规模 $S$ 为 $m$ 和 $2(n-m)$。

证明：

对于第一种情况，天平不平衡

次品必然在取出的在 $m$ 个球中，且每个球的轻重已知。故解空间为球数：$m$。

对于第二种情况，天平平衡

次品必然在没有取出的在 $n-m$ 个球中，且每个球的轻重未知。故解空间为两倍球数：$2(n-m)$。

引理2：若剩余 $k$ 步，未确定的解空间规模 $S$ 必须不大于 $3^k$。

证明：

根据信息论约束， $S$ 的规模必须满足 $\log_3 S \leq k$ 才可能有解。

于是得到 $S \leq 3^k$。

根据引理 1 可知，第 1 步结束后的两个解空间 $S$ 大小分别为 $m$ 和 $2(13-m)$。

根据引理 2 可知，第 1 步结束后还剩 2 步，则 $S\leq 3^2=9$。

故得到：

$m\leq 9\\ 2(13-m)\leq9$

$m$ 有唯一解： $m=9$。即，第 1 步的分配必须取出 9 个球进行称量。然而，奇数个球无法直接进行称重。

故，13 球问题必须添加一个标准的辅助球才有解。

注：12 球问题中 $m={8,9}$，但是 $m=9$ 的情况也一样需要辅助球。

$n$ 球问题

实际上以上的证明过程使得我们可以对 $n$ 球问题进行程序化的求解。

首先根据引理 1 和引理 2 确定 $m$ 的取值范围，如果 $m$ 是奇数，则需要辅助球，否则可以递归求解 $n-m$ 和 $m$ 两堆球。

$f(n)=f(n-m)+g(m)$

引理3：$n$ 个已知轻重的球取 $m$ 个称 1 次后的两种情况的剩余的最小解空间规模 $S$ 分别为 $\lceil m/2 \rceil$ 和 $n-m$。

证明：$m$ 个已称重的球可以通过天平上的两组内部交换部分的球来进行递归求解。其中，交换其中的一半 $\lceil m/2 \rceil$ 可以降低最多的解空间。
$g(n)=g(n-m)+g( \lfloor m/2 \rfloor)+g( \lceil m/2 \rceil)$

根据引理3，可得信息论约束

$\lceil m/2 \rceil\leq3^{S-1}\\ n-m \leq3^{S-1}$

递归求解程序

$n$ 球问题每一步递归分治，要么退化成引理1的情况（$f(n)=f(m)+g(n-m)$），要么退化成引理3的情况 $g(n)=g(m)+g( \lfloor (n-m)/2 \rfloor)+g( \lceil (n-m)/2 \rceil)$。

import math

def g(n: int, max_steps: int = 3, step: int = 1):
  if n <= 0: return 0
  m = max(1, n - pow(3, max_steps - step))
  while math.ceil(m/2) <= pow(3, max_steps - step) and m <= n:
    print(
      "{indent}[step {step}] g(n={n})\t\t[{remains}, {left} - {right}];"#+"\tremain={remains}\tleft={left}\tright={right}"
      .format(
        indent = "    " * (step - 1),
        n       = n,
        step    = step,
        remains = n - m,
        left    = m // 2 if m % 2 == 0 else m // 2 + 1,
        right   = m // 2 if m % 2 == 0 else str(m // 2) + "(+)"
      )
    )
    if step < max_steps:
      g(n-m, max_steps, step + 1)
      g(m // 2 if m % 2 == 0 else m // 2 + 1, max_steps, step + 1)
      g(m // 2, max_steps, step + 1)
    break
    m += 1

def f(n: int, max_steps: int = 3, step: int = 1):
  if n <= 0: return 0
  if step == 1 and max_steps > math.ceil(math.log(n, 3)):
      print("[Warning] Extra steps, you only need [{steps_required}] steps to solve [{n}] ball game. Auto relacing max_steps..."
        .format(
          n = n,
          steps_required = math.ceil(math.log(n, 3))
        )
      )
      max_steps = math.ceil(math.log(n, 3))
      # return
  m = max(1, n - pow(3, max_steps - step) // 2)
  if m > min(n, pow(3, max_steps - step)):
    steps_required = max_steps
    while max(1, n - pow(3, steps_required - step) // 2) > min(n, pow(3, steps_required - step)): steps_required += 1
    print("No solution!\nTO solve [{n}] ball game max_steps must be at least [{steps_required}].\nAnd [{max_steps}] steps can solve at most [{n_required}] ball game."
      .format(
        n = n,
        steps_required = steps_required,
        max_steps = max_steps,
        n_required = math.floor(3/2*pow(3, max_steps - step))
      )
    )
  while m <= min(n, pow(3, max_steps - step)):
    print(
      "{indent}[step {step}] f(n={n})\t\t[{remains}, {left} - {right}];"#+"\tremain={remains}\tleft={left}\tright={right}"
      .format(
        indent = "    " * (step - 1),
        n       = n,
        step    = step,
        remains = n - m,
        left    = m // 2 if m % 2 == 0 else m // 2 + 1,
        right   = m // 2 if m % 2 == 0 else str(m // 2) + "(+)"
      )
    )
    if step < max_steps:
      g(    m, max_steps, step + 1)
      f(n - m, max_steps, step + 1)
    m += 1
    
  return 0


# f(8, 2)
# f(4, 5)
# f(13, 3)
# f(14, 3)
f(999, 6)
# f(4, 10)

程序测试

从程序中我们可以发现 12 球存在辅助球解法（输出中，“(+)” 号表示辅助球），13 球只有辅助球解法，14球不存在 3 步内解法。4 步最多可以求解40球。

输入：f(12, 3)
输出：
[step 1] f(n=12)                [4, 4 - 4];
    [step 2] g(n=8)             [3, 3 - 2(+)];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=2)         [1, 1 - 0(+)];
    [step 2] f(n=4)             [1, 2 - 1(+)];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] f(n=1)         [0, 1 - 0(+)];
[step 1] f(n=12)                [3, 5 - 4(+)];
    [step 2] g(n=9)             [3, 3 - 3];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=3)         [1, 1 - 1];
    [step 2] f(n=3)             [1, 1 - 1];
        [step 3] g(n=2)         [1, 1 - 0(+)];
        [step 3] f(n=1)         [0, 1 - 0(+)];
    [step 2] f(n=3)             [0, 2 - 1(+)];
        [step 3] g(n=3)         [1, 1 - 1];

输入：f(13, 3)
输出：
[step 1] f(n=13)                [4, 5 - 4(+)];
    [step 2] g(n=9)             [3, 3 - 3];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] g(n=3)         [1, 1 - 1];
    [step 2] f(n=4)             [1, 2 - 1(+)];
        [step 3] g(n=3)         [1, 1 - 1];
        [step 3] f(n=1)         [0, 1 - 0(+)];

输入：f(14, 3)
输出：
No solution!
TO solve [14] ball game max_steps must be at least [4].
And [3] steps can solve at most [13] ball game.

输入：f(41, 4)
输出：
No solution!
TO solve [41] ball game max_steps must be at least [5].
And [4] steps can solve at most [40] ball game.

输入：f(4, 10)
输出：
[Warning] Extra steps, you only need [2] steps to solve [4] ball game. Auto relacing max_steps...
[step 1] f(n=4)         [1, 2 - 1(+)];
    [step 2] g(n=3)             [1, 1 - 1];
    [step 2] f(n=1)             [0, 1 - 0(+)];

彩蛋：999 个球问题最少需要 7 步解决。（https://www.zhihu.com/question/20854512/answer/16411345）

输入：f(999, 6)
输出：
No solution!
TO solve [999] ball game max_steps must be at least [7].
And [6] steps can solve at most [364] ball game.

进一步，这个问题还可以求解方案数，此处不再进一步讨论。

References

谷歌面试题之-12球称重问题- 掘金
秤球问题- 维基百科，自由的百科全书
- Wikipedia 中的结论是不考虑辅助球的。本文中则默认可以使用 1 个辅助球。
知乎上的某个回答……
12球问题到n球问题的算法解
「小球称重问题」完整版解答汇总
12枚硬币称量问题底层逻辑完美分析一亿个球你也行

思维之海

12球问题及其扩展的算法解