思维之海

——在云端，寻找我的星匙。

阅《数学之美》

In

《数学之美》是吴军的作品。
主要包括自然语言处理，信息学和搜索算法等内容。

这是Vel的读书笔记，收获+思考。

自然语言

起源时期

一个信息的原始传播模型：

等价地用幻想学语言表述为：

对于$“现实\rightarrow幻想 \rightarrow联想\rightarrow信息
”$部分。

在人类发展以后，逐渐出现了庞大的信息载体：象形文字。

然而象形文字太过于唯象（就是说，任何事物都用一个初等联想来表征），导致人类需要的记忆量很大，因此必须通过编码（联想）加以简化。

在联想过程中，又产生了复杂联想，如多方联想（聚类，一词多义），从而产生特征群。

但当我们只研究$“联想\rightarrow信息\rightarrow逆联想”$部分时。可以得出另一个结论：

翻译的可行性，是因为不同的文字系统在记录信息上的能力是等价的。

对比幻想学中对翻译的定义：

翻译：根据任意给定的想界，对特定幻想的可想特征联想称为该想界下对该幻想的翻译。

都可以发现，翻译的主要局限在于想界。也就是说，想界决定了文字的复杂度上限，而翻译并不依赖于特定的文字系统（联想群）。

接着书中介绍了罗塞塔石碑。（同名语言学习软件：Rosettastone）

  • 信息的冗余提高信息的安全性。
  • 语言的数据（语料）对翻译至关重要。

随着资源的丰富化，人类语言开始出现数字。

进一步，出现了进位制。（普遍10进制。玛雅文明使用了20进制）

  • 中国：个十百千万亿兆（大端）
  • 罗马：$IVXM$（大端相减，小端相加）
  • 印度：0123456789（隐式进制单位）

自然语言从此与数字分道扬镳。

楔形文字是最早的拼音文字。

若把中文中的拼音当作字母，则它也是一种（二维）拼音文字。
可以认为历史发展中，中文字体从抽象的图逐渐规整化，从而表意$\rightarrow$表音。

从楔形文字中传播简化出的22个字母后来演变成欧亚非大陆语言体系的主体。

词是有限而封闭的集合，语言则是无限而开放的集合。

任何语言都有语法规则覆盖不到的地方。
从而引出了语言和语法之争。

转折时期

  • 计算机能否处理自然语言？Yes。
  • 处理方法是否与人一样？Yes。

早期：

1950-170。用电脑模拟人脑。成果几乎为0。

中期：

1970-21世纪。基于数学模型+统计方法。实质性突破。

核心结论：计算机并不需要拥有类似人类的智能才能完成翻译。（唯象派）

早期的研究如下：

  • 应用层：语音识别，机器翻译，自动问答
  • 认知层：自然语言处理
  • 基础层：句法分析，语义分析

但是，由于基础分析的复杂性，研究迟迟没有进展。

可以参考：抽象语法树，以及何为语法树。自然语言的语法树所需要定义的文法规则过多。

实际上，就是因为幻想和幻想之间的联想被一个一个地处理，计算机并没有学会通用联想规则。

其次，由于文本的上下文相关，更加大难度。这类特征联想也没有被掌握。

  • 算法复杂度——上下文无关算法：$O(n^2)$；上下文相关算法：$O(n^6)$。

基于统计的自然语言处理方法，在数学模型上和通信是相通的（甚至相同的）。

统计模型

通用模型

初衷：语音识别，判定一个文字序列是否可被理解并有意义。

比如在上一章的例子中：

  • 美联储主席本·伯南克昨天告诉媒体7 000 亿美元的救助资金将借给上百家银行、保险公司和汽车公司。

这句话就很通顺【语法】，意思【词义】也很明白。

如果改变一些词的顺序，或者替换掉一些词，将这句话变成：

  • 本·伯南克美联储主席昨天7 000 亿美元的救助资金告诉媒体将借给银行、保险公司和汽车公司上百家。

意思就含混了，虽然多少还能猜到一点。【词义】

但是如果再换成：

  • 联主美储席本·伯诉体南将借天的救克告媒昨助资金70 元亿00 美给上百百百家银保行、汽车险公司公司和。

基本上读者就不知所云了。【模糊】

上面的例子体现了一个转变过程：语法——词义——模糊。

贾里尼克提出：（拓展：BCJR算法）

一个句子是否合理，就看看它出现的可能性大小如何。至于可能性就用概率来衡量。
第一个句子出现的概率大致是10-20，第二个句子出现的概率是10-25 次方，第三个句子出现的概率是10-70。因此，第一个最有可能，它的可能是第二个句子的10 万倍，是第三个句子的一百亿亿亿亿亿亿倍。

（注：为避免值太小，可以使用对数概率）

引入马尔可夫假设：（马尔可夫）

  • 假设任意一个词出现的概率只同它前面的词有关。（前驱，联想链表）

条件概率公式为

利用马尔可夫假设：

于是得到

该公式对应着二元模型（More）。

当所考虑的前驱不止一个时（一般为有限个），称为n元语法模型。

对应的简化公式为：（以三元为例）

这样的模型之所以在自然语言中很成功，是因为大多数自然语言都具有局部性。（人类的联想大多是初等的）

由于现实中，联想总是相对稀少，统计模型的成功也就不难理解了。事实上，越是重复度高，统计模型就越有用武之地。（大数定律）

比如，翻译一个几乎很少被使用的生僻词汇，可能就需要非统计学的手段。（频率将不可靠）

对于跨越上下文的”长程依赖性（Long Distance Dependency）“，n元模型将很难解析。
（n元模型的复杂度为$O(|V|^n)$，$V$是词汇量）

尽管联想稀少，但对于人工处理来说仍然是天文数字级的。（联想视界论）

接下来只需要进行文本统计，确定各个概率就行了。

为了解决统计样本不足时的概率估计问题，诞生了很多平滑性的处理。

比如，古德-图灵估计（More，More2）：从已有事件中统一分配一部分的概率给未知事件。

公式表述了Good-Turing估计的核心。其中，$N_r$指语料库中频率为$r$的词数。

$r$较大时，

  • 统计中频率$\approx$概率。

$r$较小时，我们利用Good-Turing估计，将$r$较小的词的概率进行修正。

  • 一般$N_r$和$r$的关系呈现凹性负相关（Zipf定律）
    因而$r$ 越小，$N_r$上升越快，故我们修正得到的$d_r$会比$r$小得多。（并且，有正定性：$d_0>0$）
    这样，我们实际上只把一些中等频率的词的概率分配给了生僻词。（卡茨退避法）

为了更直观的理解，我们还可以用反证法。
假如我们把前面的公式写为

可以得到

对于$\cfrac{r}{r+1}$，在$r\rightarrow0$时，极限趋于1。

而对于$\cfrac{N_{r+1} }{N_r}$，由于$N_r$和$r$凹性负相关，因此在$r\rightarrow0$时，极限趋于$\infty$。（仅负相关则不能推出）

故原假设不成立。并且，$r\rightarrow0$时，$0<d_r≪r$。

接下来只需要进行语料收集，训练模型就行了。

分词

贪心法

查字典，单向遍历字符串，每次贪心地找到最长的（字典里有的）匹配。（梁南元守创）

但是，贪心法对二义分割失效。

例：发展中国家。

字典：发，展，中，国，家，发展，中国，国家。

从左往右：发展-中国-家。
从右往左：发展-中-国家。

动态规划+统计

由底至上地利用统计数据获得最大概率出现的分词方法。（拓展：背包问题，背包九讲）

例：发展中国家。

频率字典：发（0.05），展（0.01），中（0.02），国（0.04），家（0.03），发展（0.1），中国（0.2），国家（0.15），发展中（0.4）。

状态转移方程可描述为：

其中$dp[i,j]$指分词法在区间$[i,j]$的最大概率。（仅用加法粗糙地表示）

下为初始的频率字典表。

dp[i,j] j0 1 2 3 4
i0 0.05 0.1 0.4
1 0.01
2 0.02 0.2
3 0.04 0.15
4 0.03

经过状态转移方程（5）计算后得到：（仅利用了上三角。技巧：由底向上计算）

dp[i,j] j0 1 2 3 4
i0 0.05 0.1 0.4 0.44 0.55
1 0.01 0.03 0.21 0.24
2 0.02 0.2 0.23
3 0.04 0.15
4 0.03

细节上可能还要实现回溯功能，dp[i,j]不为空时跳过……and so on

更一般地，利用Viterbi算法（More）。

介绍了颗粒度概念。

机器翻译中大颗粒度更好；网页搜索中小颗粒度更好。

Viterbi算法

维特比算法是针对篱笆网络（Lattice）的有向图最短路径提出的。（动态规划，传播式算法）

凡是使用隐马尔可夫模型描述的问题都可以用它来解码。

维特比算法的核心在于：传播。

由于维特比算法的传播特性，维特比算法可以等效为一个BFS。

如下图：（相当于一条马尔可夫链的状态伸展【上下伸展】，每一列代表原来的一个时刻）

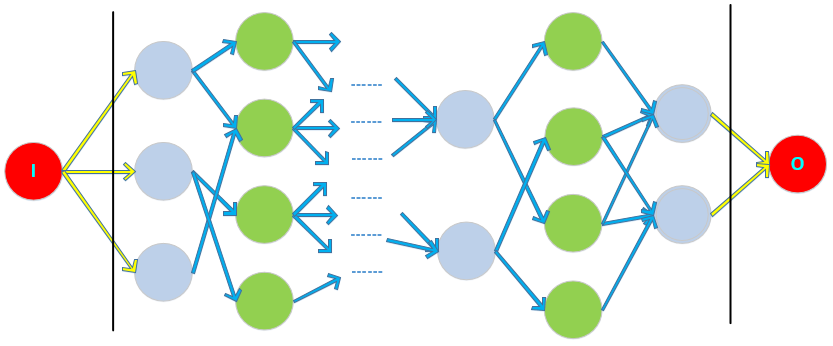
在两条竖线之间就是维特比算法的篱笆图。
维特比求的是最优值。其实就是求从左到右的最短路。
我们在左右端添加两个头尾节点（红色节点），连上一些0权的边（黄色边），即可以使用从节点$I$到$O$的BFS了。

设共有$N$列，每一列节点的最大数量记为$D$（篱笆高度），可以算出两列间边数的上限为$D^2$（篱笆间隙）。
维特比算法只须遍历所有的边，故算法复杂度为$O(ND^2)$。
（相比穷举的指数级复杂度：$O((D^2)^N)=O(D^N)$优化不少）

总之，形象地说，BFS最短路径问题掐头去尾就得到了Viterbi算法。

由于任何的语音、文字的输入都是以流（Stream）的形式进行，只要处理每个状态的速度快过讲话、打字就行。此时，解码过程将是实时的。

（我的思考）

纯粹幻想学中对幻想空间的纯化，就是一个逆向的BFS。

其次，为了结合BFS、DFS和统计学的优势，我构想了以下的算法。

有限传播算法/有限优先算法（Finite First Search，FFS）：

  • BFS只能无偏地传播，搜索进度慢，形成比较均衡的搜索树
  • DFS只能定向传播（又称为传递，因为仿佛有一个虚拟的信物/令牌在节点之间传递），容易陷入过于细分的领域，运气成分高，并且容易形成强烈失衡的搜索树
  • FFS综合了BFS和DFS，充分利用已知信息（通常信息集中于前几层），引入概率模型，在每一次搜索时选择概率最大的多个进行搜索，实现适度均衡的搜索树。（与剪枝策略相反）
  • 类似思想：随机梯度下降（Stochastic gradient descent，SGD）。
    （在有限传播中可能找不到类似梯度这样局部的全面、精准的度量。有限传播算法考虑在有限资源的前提最大可能程度地获得答案）
  • 类似算法：A*算法。（More，启发式搜索算法）

维特比本人还参与将CDMA技术（码分多址）应用于3G移动通信（More，高通公司）。

  • 频分多址（FDMA）：将不同的频率（频道）一一对应地分给用户。
  • 时分多址（TDMA）：类似时间片轮转，将同一频道切分为细小的时间片给不同用户。当切分得足够小，可近似具有实时性。
  • 码分多址（CDMA）：类似量子态叠加（或者Fourier解析），用户通过一个密匙从大量的信息中过滤出自己的信号。

注：可以认为，址就是用户，分多址就是分给多个用户（使用）。

隐马尔可夫

上文已经提到过通信模型：$【发送】信息1 \rightarrow编码\rightarrow信息2（信道）\rightarrow解码\rightarrow信息3【接收】$。

具体的，我们认为信息3和信息1是相似的。为了求取最佳信息3（解码），通过最大概然法。

假设信息1的序列：$S_1,S_2,…S_n$；信息2的序列：$O_1,O_2,…O_n$；信息3的序列：$s_1,s_2,…s_n$。

假定我们已经拥有信息1的所有可能序列（样本）。

利用相似原理和贝叶斯公式有

我们要求左式$P(s_1,s_2,…s_n)$的最大值，而$P(O_1,O_2,…O_n)$是固定的，不影响最值求解。因而我们可以简化为

最后，我们使用隐含马尔可夫模型来对上式进行估计。

马尔可夫链之前已经介绍过了。我们可以将其形成过程形象地称为“概率图灵机”。

图灵机按照一定的规则在纸带上的状态上行走；概率图灵机将每一步固定的路线选择解析成有概率的事件。

记录这些事件发生概率的总表称为“概率转移矩阵”。（实质就是带权、归一的邻接矩阵）

通过概率图灵机产生一个可观测的马尔可夫链：$S_1,S_2,…S_T$。

显然，我们可以通过统计频率的方法来估计概率转移矩阵。

但是，当观测条件受限时，则要引入隐马尔可夫。（可以想成唯象化的马尔可夫链）

隐马尔可夫：源马尔可夫链（$S_1,S_2,…S_T$，隐序列）不可观测。我们将接收到一个新序列（$O_1,O_2,…O_n$，表序列），其中满足$O_i=f(S_i)$。

注意，$O_i=f(S_i)$表示$O_i$是且仅是$S_i$的函数。（独立输出假设）

如下图所示：

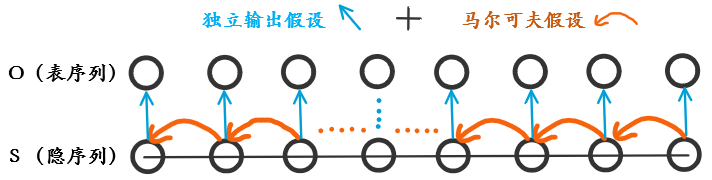
计算特定S序列产生O序列的概率：

式右边利用了马尔可夫假设【$P(St|S{t-1})$】和独立输出假设【$P(O_t|S_t)$】。

现在我们利用上式和前面的简化式的相似性完成对简化式的估计。

相似性体现如下：

至此，解码问题将能利用隐马尔可夫模型解决。

隐马尔可夫模型（HMM）有三个典型问题：

  • （预测）给定模型，计算特定O序列的概率【Forward-Backward算法】
  • （溯源）给定模型+特定O序列，估计最佳似然S序列【Viterbi算法】
  • （训练）给定观测数据，训练隐马尔可夫模型参数【Baum-Welch算法】

对于训练，可以使用监督学习获得参数$P(St|S{t-1})和P(O_t|S_t)$，但标注数据的获取成本高。

于是有了无监督的Baum-Welch算法。

同样的O序列可能对应多个HMM模型（记为$M_{i}$）。

Baum-Welch算法将试图找到其中最可能的模型$M_{\theta}$（最佳模型）。

Baum-Welch算法（迭代）：

  • 首先找到任意一个满足O序列的HMM模型$M_i$
  • 通过$M_1$可以利用O序列反向生成一个标注数据集
  • 利用标注数据集，根据隐马尔可夫（解码算法）生成新的模型$M_{i+1}$
  • 再次反向生成、生成……
  • ……
  • 直到收敛。找到质量足够好的模型$M_n$（期望最大化）
    • 用$Mn近似表示最佳模型M{\theta}$。

注意，Baum-Welch算法证明了$P（O|M_{i+1}）>P（O|M_i）$，即，每次迭代都更优。

由于一般得到的是局部最优（极值），Baum-Welch算法生成的模型可能稍逊于监督学习模型。

对于单峰的凸函数（如，信息熵），则将表现正常。

若为了确保得到全局最优，可以考虑结合遗传算法。

信息学

信息论

香农创立的信息论的基础内容不再介绍。只记录几个概念。

  • 信息熵：$H(X)=-\sum_{x\in X}P(x)logP(x)$。

  • 条件熵：$H(X|Y)=-\sum_{x\in X,y\in Y}P(x,y)logP(x|y)$。

$H(X)\geq H(X|Y)$。（可以推广。意味着n元模型的精确度高于n-1元模型）

  • 互信息：$I(X;Y)=\sum_{x\in X,y\in Y}P(x,y)log \cfrac{P(x,y)}{P(x)P(y)}$。

$I(X;Y)=H(X)-H(X|Y)$。

  • 交叉熵（相对熵）：$KL(f(x)\mid \mid g(x))=\sum_{x\in X}f(x)\cdot log\cfrac{f(x)}{g(x)}$。

交叉熵衡量差异度。差异越大，交叉熵越大。
交叉熵没有对称性。

为了获得对称性，提出了平均交叉熵：$JS(f(x)\mid\mid g(x))=\frac{1}{2}[KL(f(x)\mid \mid g(x))+KL(g(x)\mid \mid f(x))]$

应用：信号处理，同义词判断，语言模型复杂度，TF-IDF，似乎可以用来查重orz。

内容学习参见：学堂在线-《应用信息论基础》。

指导读物：通信的数学理论。（香农所著的信息论奠基性论文）

通俗读物：信息简史。（英文版）

教材参考书如下，[2]和[3]可作为延伸阅读材料：

[1] Thomas M. Cover与Joy A. Thomas著的无比经典的教材《Elements of Information Theory》（中文版书名为《信息论基础》，阮吉寿、张华等译）；
[2] Abbas El Gamal和Young-Han Kim合著的《Network Information Theory》（中文版书名为《网络信息论》，张林译）；
[3] Imre Csiszár和János Körner Csizar所著的学院派经典《Information Theory: Coding Theorems for Discrete Memoryless Systems》。

信息指纹

爬虫应用

爬取过的URL的直接存储，非常占用内存。

但通过一个散列函数，将长长的URL映射到一个128位（16字节）的随机数，将能有效地控制空间。

关键算法：伪随机数产生器算法（Pseudo-Random Number Generator，PRNG）。

现在常用的PRNG算法是梅森旋转算法（Mersenne Twister）。

这个随机数就称为URL的信息指纹。

集合判等

  • 暴力法：两两做比较，$O(N^2)$
  • 排序法：先排序，再从头至尾比较，$O(NlogN)$
  • 散列法：将第一个集合放到散列表中，然后拿第二个集合作对比，$O(N)$。但需要额外的$O(N)$空间。
  • 指纹法：对集合$S$，定义指纹$FP(S)=FP(e_1)+FP(e_2)+…+FP(e_n)$。比较即可。就地算法。

如果集合只是相似。

可以按某些规则（比如，尾号是24的电子邮件地址）随机从集合中抽取几个元素，如果两个集合的抽查指纹相同，那么它们是相似的。

也可以使用相似哈希。

反盗版（视频）

视频动辄上M、G的体量，几乎不可能采用普通的比较策略。

视频匹配的两个核心技术：

  • 关键帧提取
    • 尽管视频每秒可能有几十帧，但每一帧的差异不大。一般来说，每数秒才能提取出一个关键帧。
  • 特征提取
    • 利用信息指纹来表示关键帧，退化为集合判等问题

指纹重复

信息指纹客观地存在着极小概率的重复可能性。

假设随机数范围是$0~N-1$，共$N$个。可以推出$k$个指纹不发生重复的概率：

（我的解法）

对上式，当N很大时，分子可以用斯特林公式估计：$n!\approx \sqrt{2\pi n}(\frac{n}{e})^n$。

即：$(N-1)(N-2)…(N-k+1)=\cfrac{(N-1)!}{(N-k)!}\approx \cfrac{ \sqrt{2\pi (N-1)}(\frac{N-1}{e})^{N-1} }{ \sqrt{2\pi (N-k)}(\cfrac{N-k}{e})^{N-k} }$。

若我们有$k\ll N$（这一般是成立的，比如128位的指纹，$N=2^{128}$和$k\approx 10^{6}\approx 2^{20}$【百万级】），则可以进一步化简：（$c=e^{-(k-1)}$是一个关于$k$的小常数）

故我们得到原来的概率变为：

即，当给定$N\gg 0$和$k\ll N$时，不冲突的概率$P_k$是与$k$强相关的指数衰减函数。（当然，数值上可能并不准确）

在《数学之美》中采用的估计函数如下：

同时，若要$k$个指纹重复的数学期望超过1，则$P_k<0.5$，此时可以解得$k>\frac {-1+\sqrt{1+8Nlog2} }{2}\approx2^{64}\approx 1.8\times 10^{19}$。可能性几乎为0。

相似哈希

相似哈希是一种特殊的信息指纹。

假设一个网页有若干词$T：t_1,t_2,…t_k$，对应的权重（比如TF-IDF值）为$w_1,w_2,…_k$。计算出$T$向量的信息指纹$FP(T)$。（假设指纹为8位）

  • 扩展【将8位指纹处理为8个实数$r_i$】

    • ```c++
      for(int i=1;i<=k;++i)
      r[i] = 0;  //初始化为0
      for(int i=1;i<=k;++i) //这里在变量类型上是扩展的，但在信息上却是压缩的
      for(int j=1;j<=8;++j)
    if(t[i][j]) r[j] += w[i];  //t[i][j]是词t_i的第j位
    else r[j] -= w[i];

      1
      2
      3
      4
      5
      6
      7
      8
      9

          经过上面的处理，我们将获得一个实数向量$R=\{r_i\}$。

      - **收缩**【将8个实数$r_i$重新布尔化为8位指纹】

        - ```C++
          bool P[9];
          for(int i=1;i<=8;++i)  //进一步压缩信息
              P[i]=(bool)(r[i]);  //P向量是文章的信息指纹

  • 我们获得了可以进行相似性比较的信息指纹$P$（相似Hash）。
    若两个网站雷同，则相似哈希接近。

布隆过滤器

需求：判断一个元素是否在一个集合内。（联系之前的信息指纹部分——集合判等）

一般的散列表需要较多的容量才能存下集合中所有的元素。

布隆过滤器（Bloom Filter）仅需要散列表1/8到1/4的大小就能解决同样的问题。
它实际上是一个很长的二进制向量和一系列随机映射函数。

例：假定存储1亿个电子邮件地址，先建立一个16亿bit的向量并清零。

  • 对每一个邮件地址$X$，用8个随机数产生器$F_i$先生成8个信息指纹$f_i$
  • 然后将$f_i$用随机数产生器$G$将$f_i$映射到1~16亿的8个自然数$g_i$
  • 将$g_i$对应的bit位设置为1
  • 对1亿个电子邮件地址做相同处理

这样，一个针对这些电子邮件地址的布隆过滤器就建好了。

检测可疑电子邮件：

  • 用$F_i$转换该地址，生成信息指纹$s_i$
  • 将$s_i$用$G$映射到8个bit位，若对应为1，则命中

布隆过滤器能保证所有的命中，但可能会过度命中（一些不在集合中的元素也有极小的可能被命中）。

补救：维护一个小的白名单。

密码学

密码学的道：

  • 无论获取多少密文，也无法消除己方情报系统的不确定性。
    为了这个目的，不仅要密文之间相互无关，同时密文还是看似完全随机的序列。

注：根据信息守恒，当密文的形式越混沌，其可以携带的信息量就越少，则为了保证信息不失真，必然会在密钥（解密方法）上集聚极高的信息量。这值得权衡。

搜索

索引

搜索之道：下载、索引和排序三大步骤。

介绍布尔代数。

真值表示法：用一个2进制真值串表示关键字。（由于大量0，属于稀疏，可改用字典【关键字-真值位置】结构）

假设互联网上约$10^{10}$个有意义页面，词汇表大小约$3\times 10^5$，压缩比约$100:1$。则最终索引的大小约$3\times10^{13}$。

为了排名方便，还存有词频、词的位置等。
由于存储量巨大，故一般要采用分布式系统。

网络爬虫

根据图论的两种典型遍历方法：BFS，DFS。

互联网通过超链接（有向边）的形式连成虚拟之海。

注：可以查看我的文章了解更具体的技术：Pyspider操作指南。

网络爬虫的构建

  1. BFS或DFS？
    1. 小容量爬虫，爬取首页即可，用BFS
    2. 考虑握手（和网站建立连接）成本，在特定的网站适当采用DFS
  2. 页面分析和URL（链接）提取
    1. 通常采用队列，直接提取HTML中的URL标签
    2. 若网站采用了不规范的脚本（如JaveScript），需要通过高级模拟手段，利用浏览器内核解析网页
  3. URL记录表
    1. 用一个散列表记录已经遍历过的网页（分摊复杂度$O(1)$）
    2. 分布式系统散列表的维护和访问是难题

PageRank

质量

对于特定查询，搜索结果的排名取决于两组信息：质量（Quality）信息和相关性（Relevance）信息。

早期搜索引擎的挫折：（按解决时间排序）

  • 收录网页少，只能对常见词索引
  • 查询的结果相关性差

信任法则：指向一个网页的其它网页数量（节点的入度）越高，排名越高。（民主表决）

为了更加合理地刻画高信任高权重的相关性，采用了权重。
即，一些被链接更多的网页，链接其它网页将具有更高的影响力。（可信度）

迭代原理：给定所有网页一个相同的初始排名，利用信任法则进行迭代计算，最终排名将收敛到真实值。

由于互联网的链接是稀疏的，因此可以采用稀疏矩阵计算方法简化算法复杂度。
由于PageeRank更新一次很慢，因此诞生了并行计算方法（MapReduce）。
如果进一步考虑用户的点击数据，则可以进一步优化排名。

PageRank是一种整体化思维。

对于PageRank，就是典型的联想图，如果一个幻想所链接的其它幻想越多，说明它更常见、更重要。但PageRank仍然有其局限所在，幻想的唯象程度太高了。

而且，由于是民主表决，PageRank将具有群体惯性，即，有偏向性。

搜索的目的是了解更广阔的世界，如果一个搜索引擎是有偏的，想界的扩张自然也就受限了。此时，用户更容易陷入神经制剂的纷扰当中。

另一方面，由于人类获取信息的能力有限，搜索引擎可能要在无偏和高效之前作出权衡。（联想公平和效率）

PageRank的计算方法。

简单示意如下：

其中，$A$为带权邻接矩阵（刻画网页链接），$B$为排名向量。

设初始排名为$B_0=[\frac{1}{N},\frac{1}{N},…,\frac{1}{N}]^T$，迭代方程如下：

一般迭代10次左右就基本收敛。

MapReduce

上述问题已经抽象为了一个矩阵相乘的问题。

若要充分利用分布式系统的优势，可以采用矩阵的分治法。

另一种非严格意义上的分治是求结果矩阵的某一个元素。可以分出原两个矩阵中的对应行、列，然后再细分，将计算任务平均分配（此时分配是容易的），就能将计算时间缩短。这就是MapReduce的原理。（Map，分解任务；Reduce，整合结果）

相关性

为了解决之前提到的PageRank可能具有的唯象性，引入了相关性的度量和排序。

影响搜索引擎质量的因素：

  • 用户的点击数据
  • 完备的索引
  • 网页质量的度量（PageRank）
  • 用户偏好
  • 网页与查询的相关性

TF-IDF

TF：Term Frequency，词频。

一般采用相对词频：$\cfrac{关键词次数}{网页总字数}$。查询的所有关键词的词频相加，得到网页的相关性。
为了避免某些无意义的词的干扰（如“的”、“是”等），引入了停止词（这样的词不计入相关性统计）。
为了让一些更专业的词汇有更大的权重，引入了主题词（这样的词具有权重系数）。

由TF得到了相关性的计算公式：

为了进一步确认权重，引入了IDF。

IDF：Inverse Document Frequency，逆文本频率指数。

定义式：$IDF=log\cfrac{D}{D_w}$。（关键词$w$在$D_w$个网页中出现过，$D$是总网页数）

假如中文网页数是$D=10亿$，停止词“的”在所有网页中出现，则它的$IDF=log\frac{10亿}{10亿}=0$。
假如专用词“原子能”在200万个网页中出现，那么它的$IDF=log\frac{10亿}{100万}=8.96$。（以2为底）
假如通用词“应用”在5亿个网页中出现，那么它的$IDF=log\frac{10亿}{5亿}=1$。

于是，得到引入权重后的相关性：

从本质上讲，$IDF$是一个特定条件下关键词的概率分布的交叉熵。

权威性

提及（Mention）：在文章段落中，讨论某个主题，提及了某个名称。

当提及越多，则认为某个名称越权威。

提及隐藏在自然句中，需要自然语言处理方法。
即使有了好的算法，提及的计算仍然巨大。

另一个难点是搜索结果的权威性的排序与搜索的主题相关。

假设有$M$个网页，$N$个关键词，则需要计算和存储$O(MN)$的结果。

非常依赖于云计算和大数据技术。

计算权威度的步骤：

  • 对网页标题、正文进行句法分析，获取Mention信息
  • 利用互信息，找到主题短语和信息源的相关性
  • 对主题短语进行聚类（可用矩阵奇异值分解）
  • 对网页进行聚类，权威性的度量只能建立在子域（Subdomain）或子目录（Subdirectory）等粗略的级上。

新闻分类

更广义地讲，文本分类的任务都是基于同一个原理。

假设词汇表有N个词。

我们统计新闻中出现的词，计算它们的TF-IDF值（没有出现过的为0），就可以形成一个关于该新闻的TF-IDF向量（N维）。

利用两个新闻的TF-IDF向量的夹角，可以来反映新闻之间的相似度。

这里利用余弦定理即可。

通过这个的方法，我们可以设定一个相似度阀值，将小于阀值的新闻归到一类。在分好的小类里，又可以继续求类与类之间的相似度，从而获得更大的分类……

大数据时余弦计算的额外处理：

  • 充分利用TF-IDF向量中的非零元素
  • 删除虚词/停止词（消除了噪声）
  • 考虑词的位置加权（比如，在标题、首尾进行额外加权）

奇异值分解

上文中的余弦算法只适合于处理中大规模的文本（百万级），对于超大规模文本（亿级），则需要相对快速、粗糙的算法。

之前的新闻分类本质上是一个聚类问题，但是需要每个向量两两做计算。我们希望有一个办法——一次性地计算出所有的相关性——矩阵奇异值分解（Singular Value Decomposition，SVD）。

我们需要一个超大的矩阵$A_{M\times N}$来描述成千上万的文章和上百万的词的关联性。

奇异值分解：（$r≪M,r≪N$）

$X_{M\times r}$：每一行（M）代表一个词，每一列（r）表示一个语义相近的词类。（元素值代表相关度）

$Y_{r\times N}$：每一列（N）代表一篇文本， 每一行（r）对应一个主题。

$B_{r\times r}$：表示词类和文章类（主题）的相关性。

只要对$A_{M\times N}$做一次奇异值分解，就可以同时完成近义词分类和文章分类，还能得到相应的相关性。

地图定位

智能手机的定位、导航：

  • 利用卫星定位
  • 地址的识别
  • 根据起点和终点，规划最短或最快路线

有限状态机

有限状态机用于地址的识别。

简单来说，有限状态机能够在有向无环状态图中不可逆地转换，当转换失败时则地址无效。

为了让识别具有一定的容错性（输错了一点仍然能够查询），提出了基于概率的有限状态机。（与马尔可夫链基本等效）

其它应用：Google Now。

动态规划

对于导航系统，一般会采用动态规划的办法。

从A点到B点的路线，一定会经过一个里程数不断增长的过程。也就是说，这是一个传播问题。因此，全局的最优，一定也是局部里程圈的最优。至此，形成了状态转移。

有限状态传感器

加权有限状态传感器：Weighted Finite State Transducer，WFST。有限状态机中的每个状态由输入和输出符号定义。

任何一个词的前后二元组，都可以对应到WFST的一个状态。

若在符号序列中某个时刻前后出现了形如$AB$的有序对。（相当于A是输入，B是输出）
则根据在有限状态机中对应的$…\stackrel{A}{\longrightarrow} STATE_i\stackrel{B}{\longrightarrow} …$结构，进入对应$STATE_i$状态。

可用于语音识别。

SEO与作弊

SEO就是搜索引擎优化。

SEO一般要适当，遵循搜索引擎的规则。

一个无所不用其极的SEO优化就称为在搜索引擎中的作弊。

早期作弊手法：

  • 重复关键词
    • 利用TF的相对词频
  • 买卖链接
    • 识别链接的流通
    • 利用出链（Out Links）向量，通过余弦算法聚类，识别卖链接的网站

利用通信模型解决搜索反作弊：

  • 从信息源出发，加强通信（编码）自身的抗干扰能力
    • 利用相反的信号抵消噪音
    • 搜集一段时间的作弊信息后，还原其原有的排名
  • 从传输来看，过滤掉噪音，还原信息

利用图论：

  • 互相链接的节点称为Clique，发现Clique并直接应用到反作弊中

利用浏览内核解析：

  • 对于使用JavaScrpt跳转页面，其落地页（Landing Page）质量非常高，但进入之后会立即通过JS程序被跳转到商业网站

反作弊是自动、无偏的。根本是去噪声。
一个网站的内容质量，决定其排名。
越流行的搜索引擎，SEO越风行。

搜索广告

搜索广告的三个阶段：

  • 竞价排名（Overture、百度）
  • 利用经验预估点击率（Click Through Rate，CTR），预测用户的点击概率
  • 逻辑回归模型

逻辑回归模型：将一个事件出现的概率逐渐适应到一条逻辑曲线（Logistic Curve）上。

一个简单的逻辑回归函数：$f(z)=\cfrac{e^Z}{e^Z+1}=\cfrac{1}{1+e^{-Z} }$。（指数模型）

逻辑回归的定义域在$(-\infty ,+\infty)$，值域在$(0,1)$。

对于$(-\infty ,+\infty)$，对于任何信号都可进行回归。
而对于$[0,1]$，可以看作概率函数，于是逻辑回归与概率分布联系起来。

对于预估点击率而言，假设$k$个影响变量$x_1,x_2,…,x_k$。

则可线性组合得到$z=\beta_0+\beta_1x_1+\beta_2x_2+…+\beta_kx_k$。

${\beta_i}$向量就是该模型的参数向量。可以通过神经网络训练得到。比如最大熵模型的$GIS$或者$IIS$算法。

数学模型

  • 一个正确的模型应当在形式上是简单的
  • 一个正确的模型最开始可能并不如复杂的错误模型准确
  • 大量的准确数据对研发很重要
  • 正确的模型可能受到噪声干扰，此时应坚定信心，积极找寻噪声源

最大熵模型

最大熵原理（The Maximum Entropy Principle）：在已知信息的基础上，不做任何主观假设，使未知事件的预测信息熵最大。此时的概率分布称为最大熵模型。

这里的熵是信息熵。

保留全部的不确定性，将风险降到最小。

希萨证明：对任何一组不自相矛盾的信息，最大熵模型存在且唯一。（其形式是指数函数）

例如：根据$w_1,w_2$预测$w_3$。

$P(w_3|w_1,w_2,s)=\cfrac{1}{Z(w_1,w_2,s)}e^{\lambda_1(w_1,w_2,w_3)+\lambda_2(s,w_3)}$.
（$Z$是归一化因子，保证$P$概率归一，与参数$\lambda_i$一起需要被训练出来）

但是，最大熵模型的计算量相当大。

比如，若搜索的排序需要考虑20种特征。

待排序的网页是$d$。

则有最大熵模型：

其中，归一化因子为

（参数$\lambda_i$通过模型的训练得到）

最原始的最大熵模型训练方法是通用迭代算法（Generalized Lterative Scaling，$GIS$）。

  • 假定第零次迭代的初始模型为等概率的均匀分布（类似PageRank的设定）
  • 用第N次迭代的模型来估算每种信息特征在训练数据中的分布，比较并调节相应模型参数。
  • 重复，直至收敛。

GIS算法是一个典型的期望值最大化算法（Expectation Maximization，EM）。

GIS收敛缓慢，而且不稳定，因此很少有人真的使用。

后来出现了改进迭代算法$IIS$（Improved Iterative Scaling），训练时间缩短了1至2个量级。

吴军提出了更快的最大熵模型快速算法，训练时间再次缩短了1至2个量级。

文艺复兴公司（Renaissance Technologies）：利用最大熵模型和其它一些先进的数学工具，成为了世界上最成功的对冲基金公司。

注意：更多相关知识可了解量化交易。

条件随机场

句法分析（Sentence Parsing）：

  • 一是指根据文法对一个句子进行分析，建立其语法树，即文法分析（Synatactic Parsing）；
  • 二是指对一个句子中各成分的语义进行分析，得到对这个句子语义的一种描述（语义树），即语义分析（Semantic Parsing）。

这里主要讨论文法分析。

Eugene Charniack提出原则：选择文法规则，让被分析的句子的语法树概率达到最大。

拉纳帕提则进行了进一步的优化，真正将数学模型和文法分析结合起来。

  • 对任意一个句子进行分词
    • 美联储|主席|本·伯南克|昨天|告诉|媒体|7 000 亿|美元|的|救助|资金|将|借给|上百|家|银行|、|保险公司|和|汽车公司
  • 扫描（从左往右），整合出高一阶的词组
    • （美联储主席）|本·伯南克|昨天|告诉|媒体|（7 000 亿美元）|的|（救助资金）|（将借给）|（上百家）|（银行、保险公司和汽车公司）
  • 重复扫描，整合……
    • 【美联储主席本·伯南克】|昨天|告诉|媒体|【7 000 亿美元的救助资金】|（将借给）|【上百家银行、保险公司和汽车公司】
  • 直到仅剩一个括号为止

容易看出，每次扫描，句子成分数按一定比例缩减，因而这个方法的复杂度是$O(n)$线性的。

上述方法对于模糊的语言处理能力较弱，为了处理更加随意的文法分析，逐渐形成了浅层分析（Shallow Parsing），找到句子中主要的词组已经它们对应的关系即可。

条件随机场使得浅层分析的正确率大大提高。（栅栏图）

条件随机场是隐马尔可夫模型的多元推广版本，此时观测序列的Oi将与前后的状态都相关，即与$S{i-1},S_i,S{i+1}$相关。（S序列仍然是马尔可夫链，但独立输出假设被推广了）

条件随机场是无向图。仍然遵循马尔可夫假设。

整个条件随机场的量化模型就是O序列和S序列的联合概率分布$P(O,S)$：

由于变量过多，不可能有足够的数据来估计这个高维分布。因此，一般要降维处理，通过一些边缘分布（如$P(O_1)$，$P(S_2)$，$P(O_1,S_3)$等）来找出一个符合这些条件的概率分布（通常不止一个满足）。

根据最大熵原理，希望找到一个满足所有边缘分布的熵最大的模型（指数模型）。

每一个边缘分布对应指数模型中的一个特征$f_i$（Feature）。（$f_i$的参数可以使用最大熵算法训练）

比如：边缘分布$f_i(O_1,O_2,…,O_n,S_1,S_2,…,S_m)=f_i(x_1)$。

将特征运用到模型之中，有

这时就可以进行浅层文法分析了。（例：Google的文法分析器Gparser）

贝叶斯网络

马尔可夫链是状态序列，每个状态值取决于前面有限个状态。

在现实生活中，关系可能是复杂、错综的，形成一个有向图网络。

若在这个网络之中，每一个状态只跟与其直接相连的状态有关，则称为一个贝叶斯网络。

贝叶斯网络是马尔可夫链的推广。

使用贝叶斯网络必须确定网络的拓扑结构，和各种状态之间的转移概率。

得到拓扑结构称为结构训练，得到转移概率称为参数训练。

从理论上说，贝叶斯网络是一个NP完全问题（现有计算机不可计算）。

但对于某些应用，经过适当简化（如，贪心+蒙特卡洛，利用互信息简化网络等），训练也能被计算机完成。

如Google的Rephil，通过贝叶斯网络完成对词、概念（词类）、文章的联系，将上千万关键词合成了上百万概念的聚类。

人工神经网络

下图来自Here，展示了一个典型的四层人工神经网络（多层感知机）的运作方式：

多层感知机

可以认为神经网络是一种特殊的有向图（90度左旋后的篱笆图）。

  • 所有节点分层，每一层通过有向弧指向上一层节点，但同一层无弧连接，不跨层连接
  • 每条弧有一个权重
  • 完了

神经元函数：为线性模型增加一次非线性变换，从而增强神经网络的分类能力。

感知机

感知机：一个输出层，一个输入层。一个计算夹层。最简单的神经网络。

感知机

详细内容直接参考Here吧。

Minsky指出)：感知机无法解决异或问题。（More）

多层感知机

实际上神经网络的计算过程就是矩阵运算。相当于：

为了基于线性分类实现复杂的非线性分类，多层的神经网络采用复杂函数拟合，利用隐藏层完成非线性空间到线性的变换。

一般来说，层数越多，神经网络的效果越好。（如下图）

神经网络入门

神经网络浅讲：从神经元到深度学习

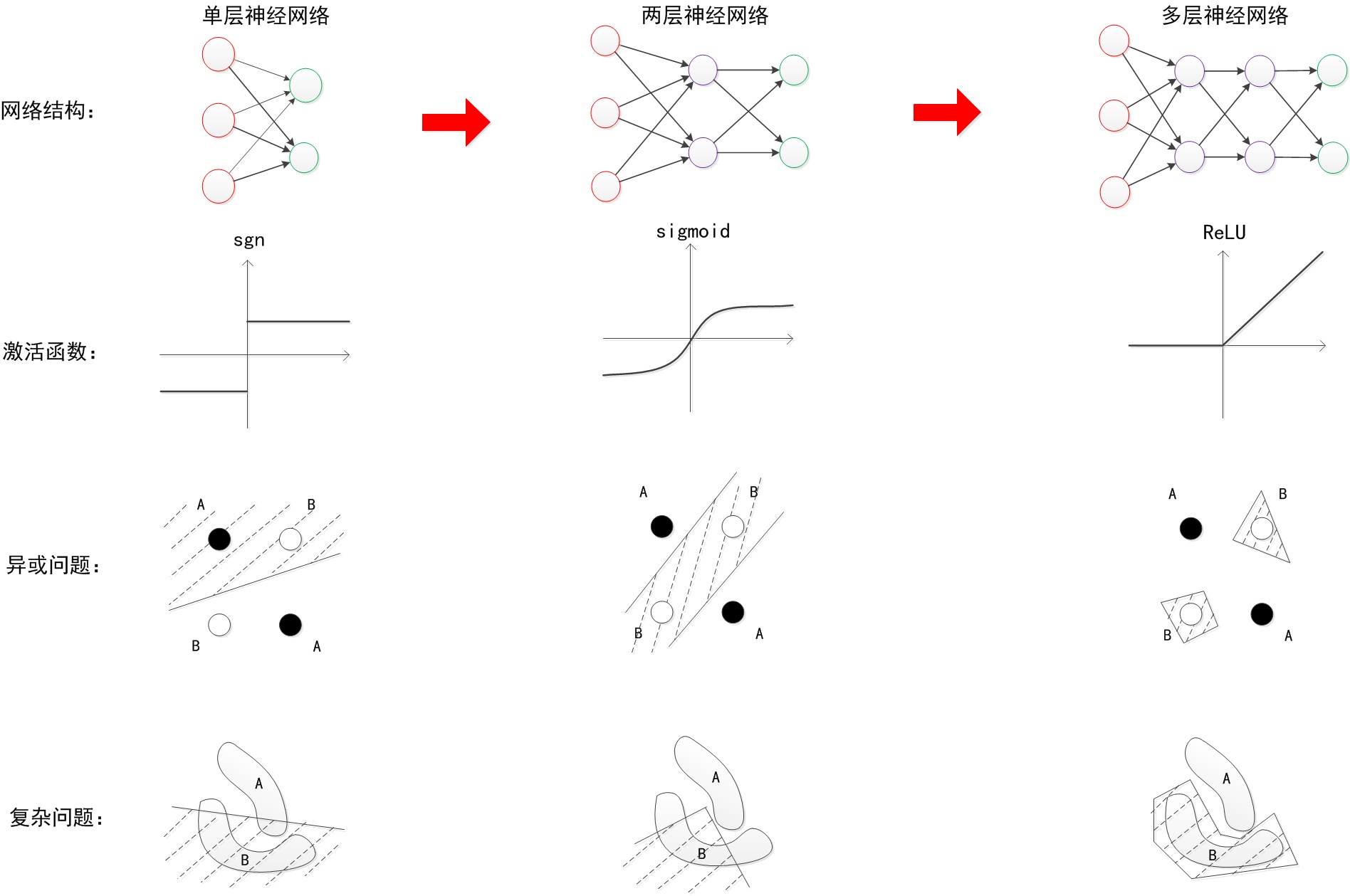
期望最大化

期望最大化算法（Expectation Maximization Algorithm，EM算法）是上帝的算法。

前面已经介绍过两种文本分类算法：

  • 利用事先设定好的类别对新的文本进行分类
    • 需要事先设定好类别和文本中心（Centroids）
  • 自底向上地将文本两两比较进行聚类
    • 计算时间较长

基于EM算法，提出了一种新的迭代算法（无须事先设定，无须聚类）。

  • 随机挑选类别的中心，然后反复优化直到收敛
    • 要利用到文本TF-IDF向量和余弦算法

记同一类中各个点到中心的平均距离为$d$，不同类中心之间的距离为$D$。

我们希望每次迭代，$d$变小，$D$变大。

假设第1类到第K类中分别有$n_1,n_2,…,n_k$个点。每一类到中心的平均距离为$d_1,d_2,…,d_k$。

则有总平均距离

同理

假定有一个点$x$，它在前一次迭代中属于第$i$类，下一次迭代后被被安排到第$j$类。

不难证明，

Baum-Welch算法（隐马尔可夫链），GIS算法（最大熵模型）都是典型的EM算法。

EM算法的分布描述：

  • E过程（Expectation）：根据已有模型，计算观测数据输入到模型的结果
    • Baum-Welch：计算每个状态转移的次数和输出的次数
    • GIS：计算每一个特征的数学期望值
  • M过程（Maximization）：重新计算模型参数，以最大化期望
    • Baum-Welch：根据这些次数重新估计隐含马尔可夫模型的参数
    • GIS：根据数学期望值和实际观测值的比，调整最大熵模型参数

EM算法优化的目标函数必须是一个凸函数，才能确保得到全局最优解。

就到这里吧。