林伟在《人工智能的新数学》主题报告中,指出人工智能中经典的数学工具,有以下四类:
- 概率论、数理统计;
- 数值代数、数值分析、最优化;
- 经典分析、函数论(比如深度学习的逼近论相关知识);
- 计算机科学基础,包括离散数学、理论计算机科学。
经典数学工具对于学生而言,是最应该掌握、最核心的工具。
References
这里面也提到了人脑的系统1和系统2(系统1 / Intuitive 是现在的深度学习,系统2 / Logical 是未来的研究方向)。
泛函分析
巴拿赫空间
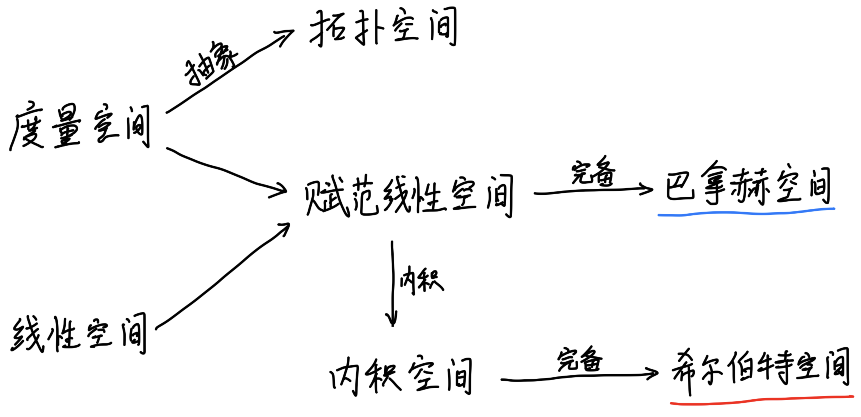
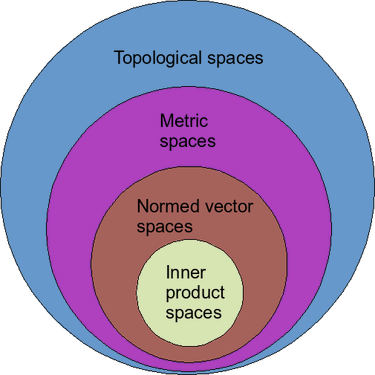
度量:$X$是一个集合,度量是$X$上的一个二元关系($X \times X \rightarrow R$),对于任意的 $x, y, z \in X$:
- 非负:$\rho(x, y) \geq 0$,(非退化)当且仅当 $x=y$ 时等号成立
- 对称:$\rho(x, y)=\rho(y, x)$
- 三角不等式:$\rho(x, z) \leq \rho(x, y)+\rho(y, z)$ 。
范数:范数是一种线性空间上的度量,它还满足
- 齐次:对于所有 $\mathbf{v} \in V$ 和 $\lambda \in \mathbb{R},$ 有 $|\lambda \mathbf{v}|=|\lambda| \cdot | \mathbf{v} |$
内积:内积是一种线性空间上的范数,它还满足
- 分配律:对于所有向量 $\mathbf{u}, \mathbf{v}, \mathbf{w} \in V,$ 都有 $\langle\mathbf{v}, \mathbf{w}+\mathbf{u})=\langle\mathbf{v}, \mathbf{w}\rangle+\langle\mathbf{v}, \mathbf{u}\rangle$
核技巧(Kernel Trick)就是一种内积。
其中,$\phi(x)$是指将样本向量 $x$ 从输入空间映射到特征空间(希尔伯特空间),从而在高维线性可分。因为我们不需要知道$\phi(x)$的具体形式,所以可以直接通过定义核函数$K(x,y)$的方式获得$\phi(x)$的隐式定义。
Q: 那么如何确定 $\phi(x)$ 映射到一个高维空间呢?
A: 这部分需要查阅核函数的理论推导。
比如,
- 线性核,其实就是没有映射
- $\kappa\left(x{1}, x{2}\right)=\langle x 1, x 2\rangle$
- 高斯核函数,也称径向基(RBF)函数,使用最为广泛,它能够把原始特征映射到无穷维
- $\kappa\left(x{1}, x{2}\right)= \exp \left(-\gamma\left|\mathbf{x}{1}-\mathbf{x}{2}\right|_{2}^{2}\right)$
- 多项式核函数,它能把数据映射到$C_{n+d}^{n}$维
- $\kappa\left(x{1}, x{2}\right)=\left(\left\langle x{1}, x{2}\right\rangle+R\right)^{d}$
完备:一个完备空间中的任何柯西序列都收敛在该空间之内。
从函数到无穷维
【直观详解】让你永远忘不了的傅里叶变换解析 Fourier 变换是将时域信号转换为频域信号,Fourier 解析是将频域信号转换为时域信号。
*脉冲
脉冲函数:Dirac函数。
高斯核背后的映射
不妨设在一维空间。如图,两个样本点:
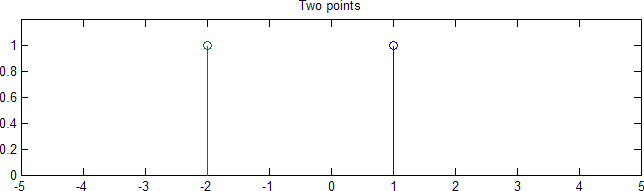
将点映射成一个函数 / 分布:(类傅里叶解析)
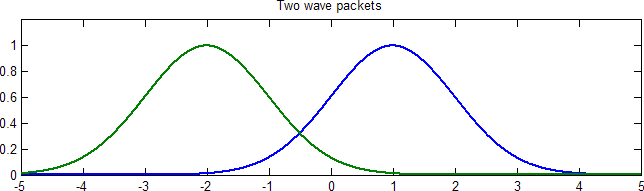
此时,函数空间构成了一个无穷维空间。
可以想象一个无限细分的柱形图,每一根立柱就是一个维度。
比如,将样本${\color{red}{x_1} },{\color{blue}{x_2} }$映射为两个高斯分布,
定义函数内积为相乘后的积分:
忽略掉系数,就得到了一个高斯核。
无穷宽的DNN
We develop Banach spaces for ReLU neural networks of finite depth L and infinite width. The spaces contain all finite fully connected L-layer networks and their L2-limiting objects under bounds on the natural path-norm. Under this norm, the…
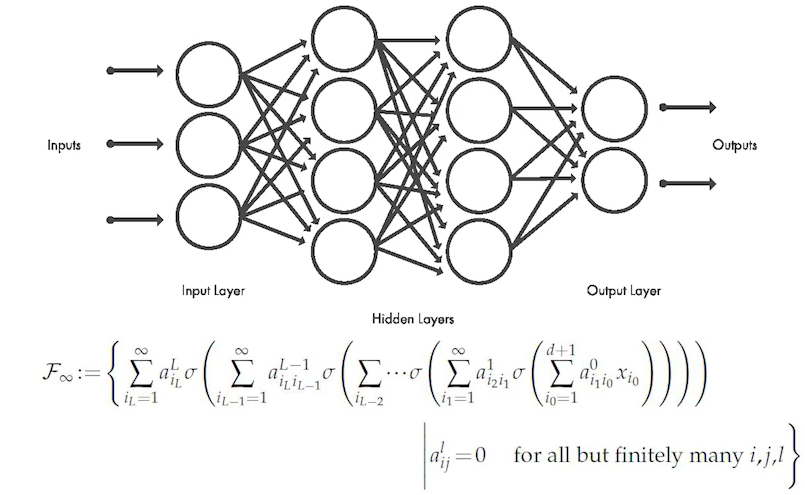
因为宽度无穷宽,就构成了一个无穷维的巴纳赫空间(完备的赋范线性空间)。
群表示论与范畴论
关于群的研究
一个群就是一个代数系统。
现代数学研究群的结构一般有两种方法:
- 研究子群
- 3b1b视频:群论与 808017424794512875886459904961710757005754368000000000
- 对有限群的基本群即单群(Simple groups)进行分类
- 有限群就是有限个元素构成的群
- 2004年由一篇100多位数学家写成的1200多页的Paper收尾
- $\Longrightarrow$ 有限单群分类定理

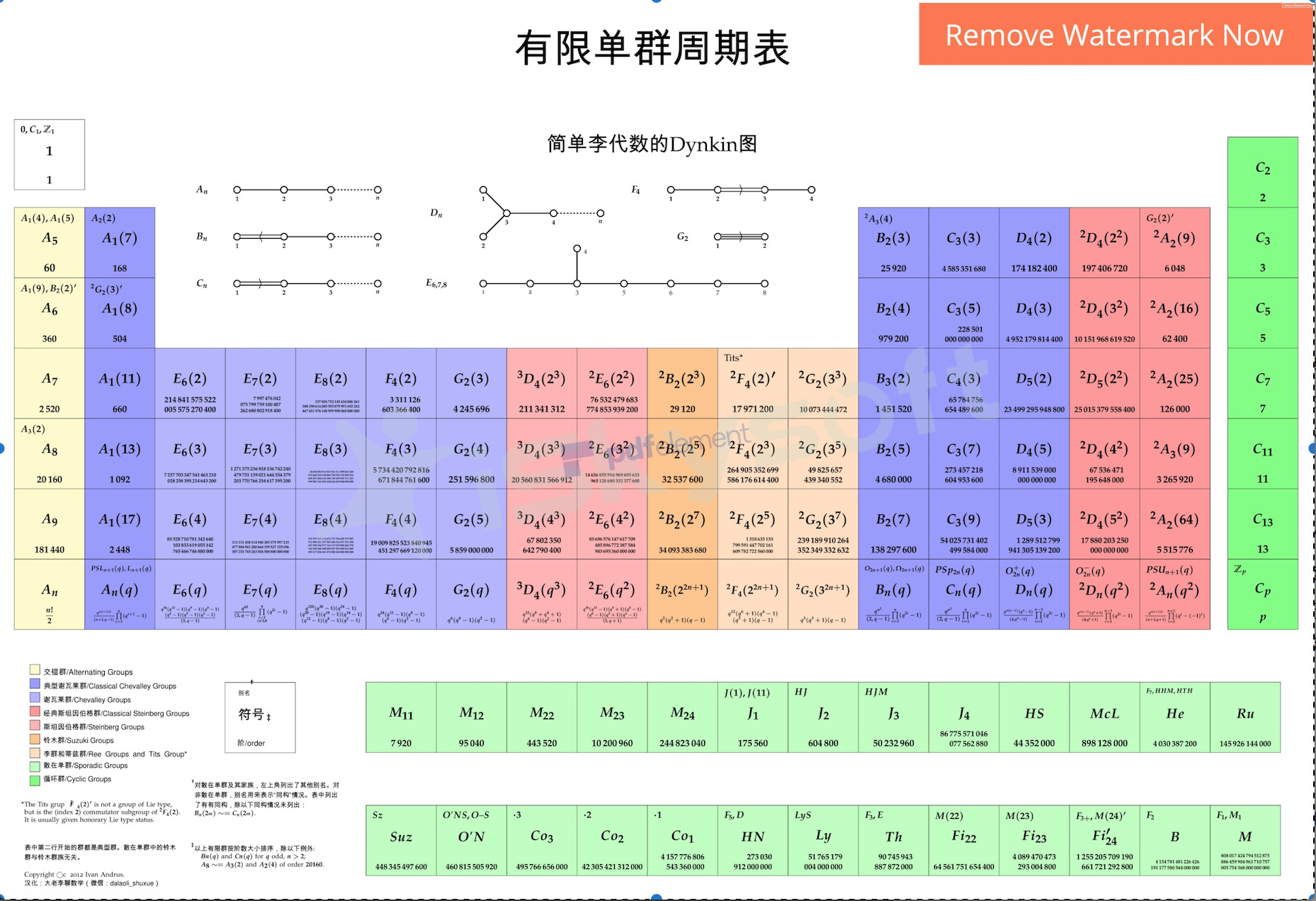
- 研究群的表示
- 群的表示就是把给定的群$G$同态地映到另一个群$W$的操作(同态就是保持运算)。
- 通过不同的表示,我们可以通过各种熟悉的$W$,来从不同的角度观察$G$的性质,从而认识未知的事物
- 什么样的群表示最值得研究?
- 不可约表示:一个表示被称作不可约的,当且仅当它没有在G的作用下不变的非平凡子空间。
- 群的表示就是把给定的群$G$同态地映到另一个群$W$的操作(同态就是保持运算)。
同态映射反映了两个代数系统的被映射部分的局部相似性(即同种规律在不同体系下的表示)。
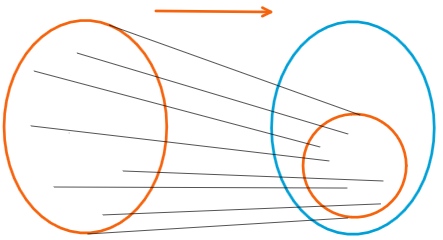
从图到范畴论
范畴论使用图论作为描述工具,节点表示一个对象,有向边表示态射,整个图构成一个范畴。
范畴,就是具有代数结构的有向图。
范畴论是“数学的数学”,它试图研究各种数学结构之间的联系和共性。
函子(Functor):如果范畴本身也作为一个对象,那么就可以创造更高阶的范畴,在这样的高阶范畴中的态射称为函子。
自然变换:把函子也作为一个对象,函子和函子间的态射就称为自然变换。
设C和D是范畴,F和G是C和D之间的函子。一个从F到G 的自然变换η,对C中每个对象,给出一个在D的对象间的态射ηX : F(X) → G(X),称为η在X处的分量(component),使得对C中每个态射f : X → Y都有:
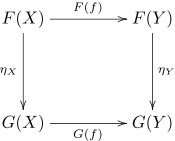
DNN中的对称性、函子
Analytic Characterization of the Hessian in Shallow ReLU Models: A Tale of Symmetry
Backprop as Functor: A compositional perspective on supervised learning
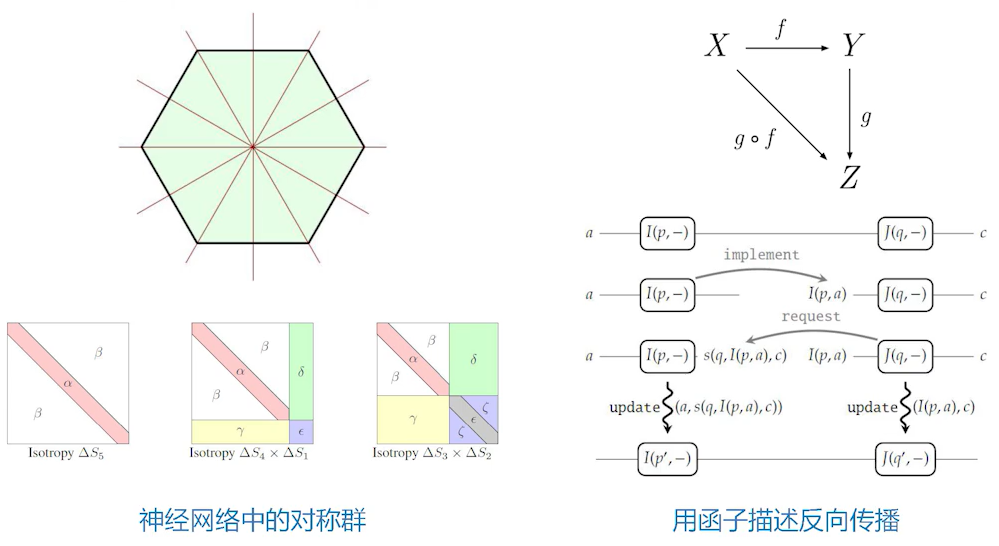
神经网络中存在一些冗余,这些冗余可以利用群表示论的技术进行一些修剪。
函子(Functor)适合于用来表达函数的复合。
微分几何
Information Geometry and Its Applications: Convex Function and Dually Flat Manifold
A Thorough Introduction to The Theory of General Relativity 前12节课
A Visual Introduction to Differential Forms and Calculus on Manifolds
微分流形
流形(Manifold):可以局部欧几里得空间化的一个拓扑空间。
希尔伯特空间就是欧几里得空间推广到无穷维。
比如,李群是一个在拓扑群上加上了微分结构的代数结构,让拓扑群的拓扑空间成为微分流形。
李群既是群也是流形。
可微流形上的微积分研究被称为微分几何,利用微积分理论研究空间的几何性质。
深度学习的几何解释
Geometric Understanding of Deep Learning 顾险峰团队
A Geometric View of Optimal Transportation and Generative Model
流形分布律:不同的类对应着流形上的不同概率分布,这些分布之间的距离大到足够将这些类区分。
顾险峰在公众号文章《基本工程问题是否需要前沿几何理论?》中提到:
大数据的本质模式可以概括为如下的物理定则(Physics law):
- 一类自然数据可以被视作嵌入在高维空间中的低维流形上的概率分布。
深度学习具有两个主要任务:
- 一是学习流形结构,表示为编码和解码映射,流形的参数空间就是隐空间或者特征空间;
- 二是概率分布变换,即将白噪声变换成数据分布。
深度神经网络的唯一功能就是表达欧式空间之间的连续映射,因此在统计深度学习领域,所有的数据都被表示成映射,概率分布也被表示成映射,即从白噪声到给定概率分布间的传输变换(transportation map)。由此,统计深度学习可以由范畴语言来表述,其范畴为{流形上的概率分布,流形间的映射}。
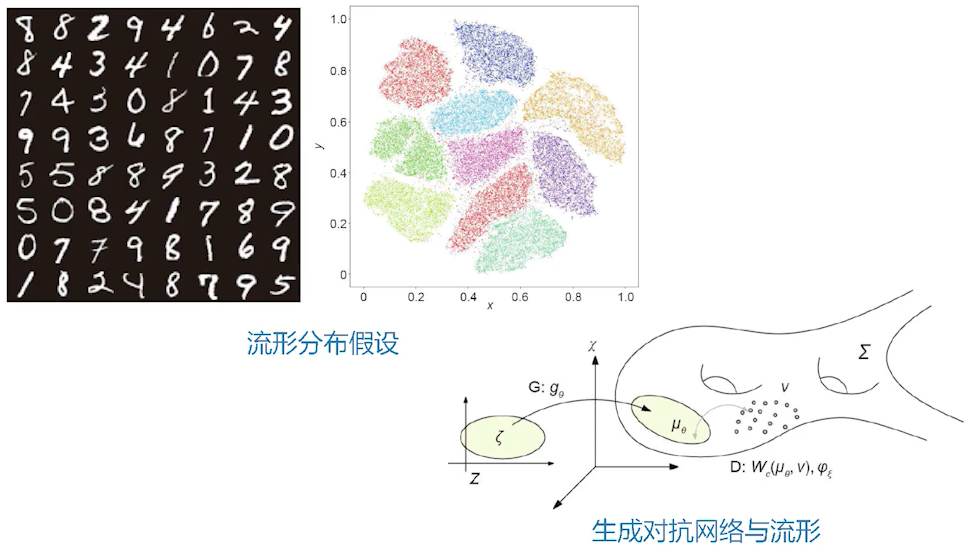
利用流形上的数学来研究GAN中从输入到输出之间的一些关系。
计算共形几何与最优传输
最优传输散度
最优传输的问题便是,有两个概率分布,怎样从一个概率分布迁移到另外一个概率分布?所以它也叫“推土机”,类似推土机一样把分布以最小的代价变成另外一个概率分布;目标是要解一个问题,每一点移动有一个代价,要使得这个移动总代价是最低的。
最优传输可以用来描述两个概率分布之间的距离,称为最优传输散度,即:Wasserstein Distance。跟统计学中KL散度的作用类似;但是,KL散度有一些缺陷:没有对称性,无法衡量离散分布和连续分布的距离……
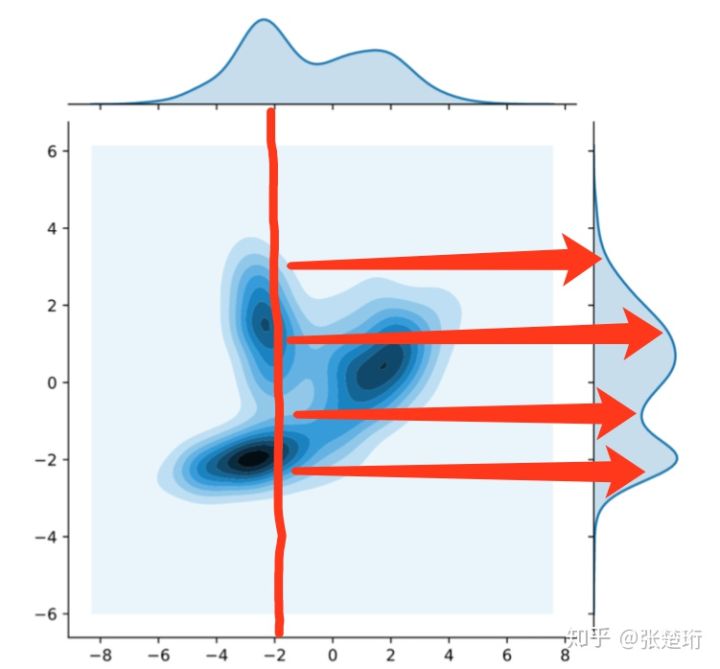
GAN的模式崩溃
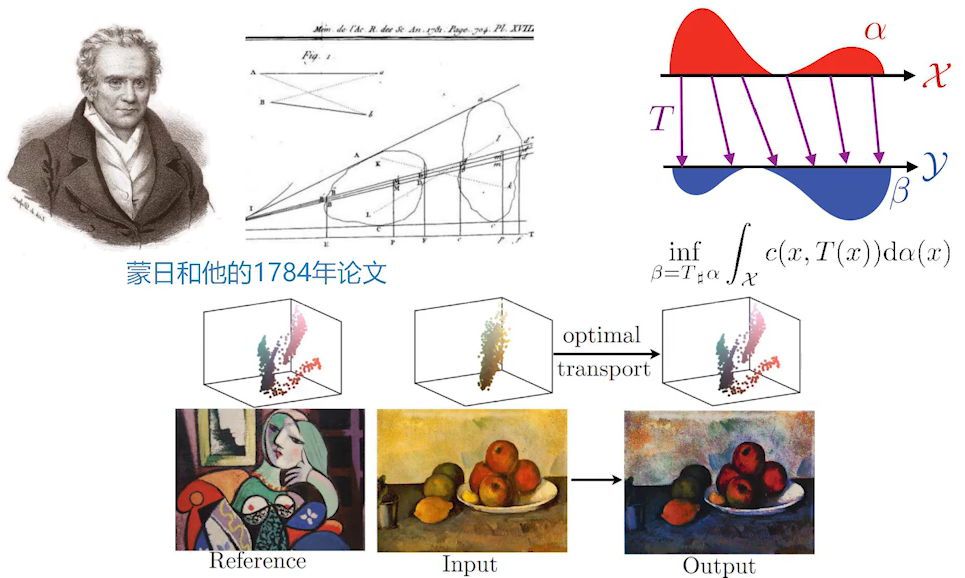
最优传输特别适合用来描述对抗生成网络(GAN)里面的问题。
这部分研究也是顾险峰团队在推动。
GAN的训练中有一种被称为模式崩溃(Mode Collapsing)的现象。GNN在学习多模态(mode)的分布时,经常只能收敛到其中的部分模态。即使经过正则一类的措施能够让GAN覆盖所有模态,却会生成虚假的样本。
顾险峰团队认为,其中的本质原因是,深度神经网络只能表示连续映射,而最优传输映射整体是非连续的。
代数几何
代数几何的基本研究对象是在任意维数的(仿射或射影)空间中,由若干个代数方程的公共零点所构成的集合的几何特性。
热带几何
热带几何是分片线性化的代数几何。
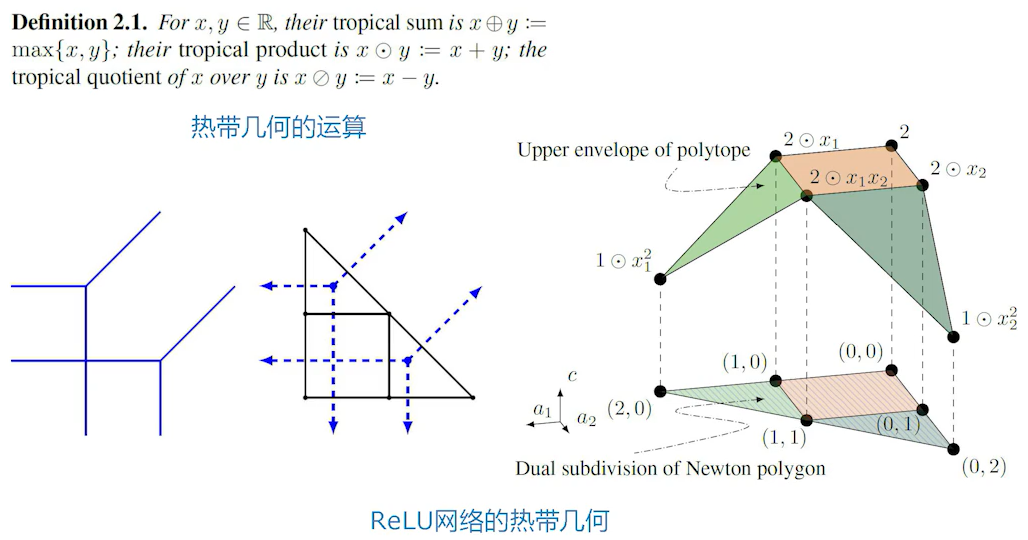
因为ReLU函数是{X,0}取大,通过这个取大操作以及加法、减法,定义了一些热带几何上的运算,通过这几种预算,我们就可以定义一种多项式。多项式就涉及到了代数几何的研究范畴。
计算机代数
向量空间、符号空间
在第三代人工智能模型中,指出两天发展人工智能的道路:
- 继续研究向量空间
- 最大挑战:语义丢失问题
- 走回知识驱动 + 数据驱动 $\longrightarrow$ 符号空间
- 在符号空间中,数学工具有限
- 朱军:符号空间的数学工具,将来大家将学习离散数学(数理逻辑),CS的还要学形式语言与自动机,组合数学,图论等相关课程,抽象代数(群、环、域)也相关
- 缺少知识
- 在符号空间中,数学工具有限
多项式代数
计算机代数主要指多项式代数,它实现了无精度损失的符号计算。属于符号空间中的数学工具。
计算机代数中常用的方法有Groebner基,三角列和柱形代数分解。
机器证明的底层数学工具就是计算机代数。
随机矩阵
A Random Matrix Approach to Neural Networks
随机矩阵:一个矩阵中的所有元素都是随机变量。
经验谱分布函数(ESD):设 $\mathrm{A}$ 是一个具有 $n$ 个实特征根的 $n$ 阶方阵,记其特征根为 $\lambda{1}, \cdots, \lambda{n}$。这些特征根的分布可以用以下函数$F_n(x)$表示,称为方阵 $\mathrm{A}$ 的经验分布函数。($I$ 为指示函数)
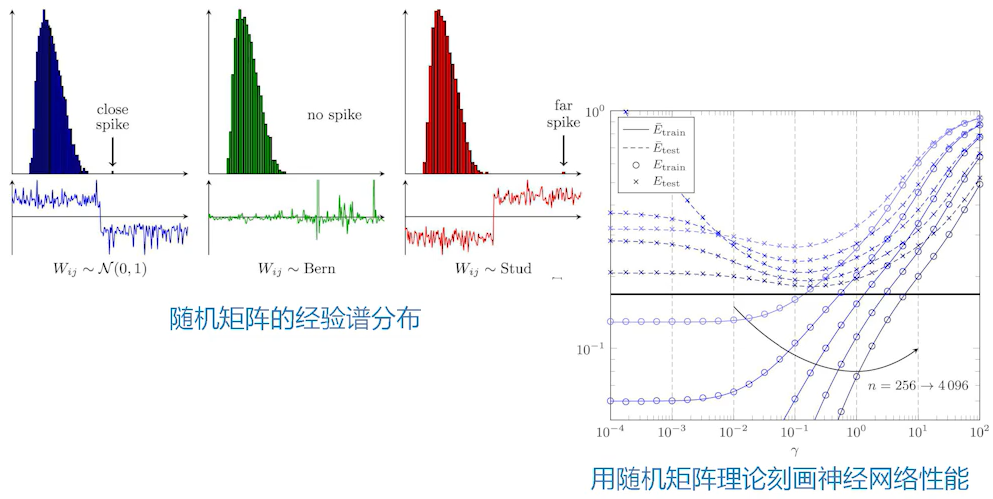
大型神经网络的权值在某些情况下接近于随机分布。可以利用随机矩阵理论来刻画它的谱分布的一些性质。
动力系统与随机分析
ResNet
ResNet的作者何凯明因为ResNet工作摘得CVPR2016最佳论文奖。
深度神经网络在加深层数时,除了过拟合、梯度消亡、爆炸的问题以外,还会遇到退化的问题(Degradation problem)。
残差学习(Residual learning):定义学习到的特征为$H(x)$,而残差为$F(x)=H(x)-x$。现在神经网络学习$F(x)$ instead of $H(x)$。
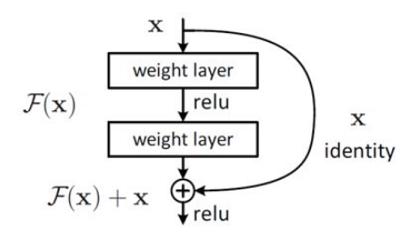
通过引入短路机制,残差网络的内部结构只需学习残差。当残差为0时,变为恒等映射。
因为残差的数量级较小,映射对于残差微小的变化较为敏感。
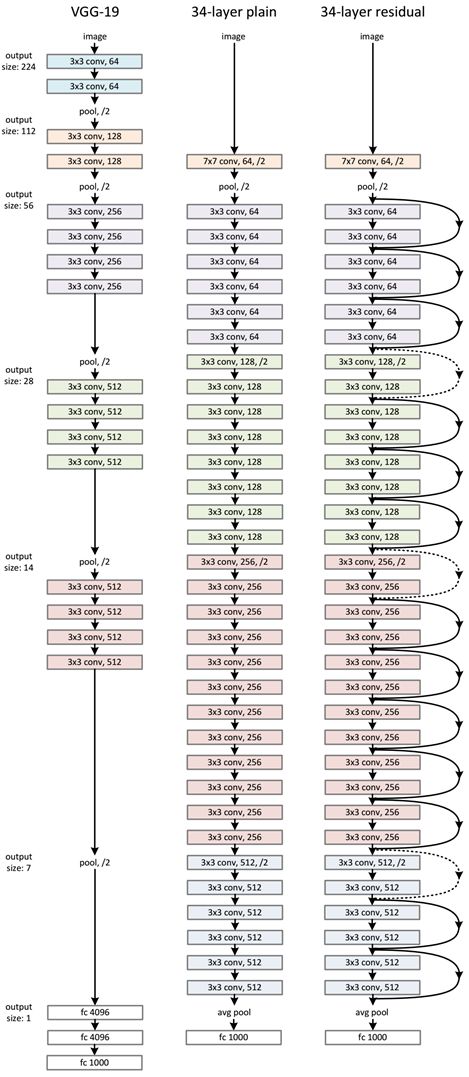
相平面图
相平面法是一种基于时域的分析方法。表示有两个独立变量的系统(二阶系统)的轨迹。
郎之万动力学
朗之万动力学 ( Langevin Dynamics ) 是控制模拟系统能量的一种常用算法。
在模拟一个大型系统时,误差会逐渐积累,朗之万动力学的实现方法是在系统中加入耗散力和随机力(相当于引入布朗运动),弱化系统误差,使得系统保持一定的平衡状态。
相关工作
Stable Architectures for Deep Neural Networks
Non-convex learning via Stochastic Gradient Langevin Dynamics: a nonasymptotic analysis
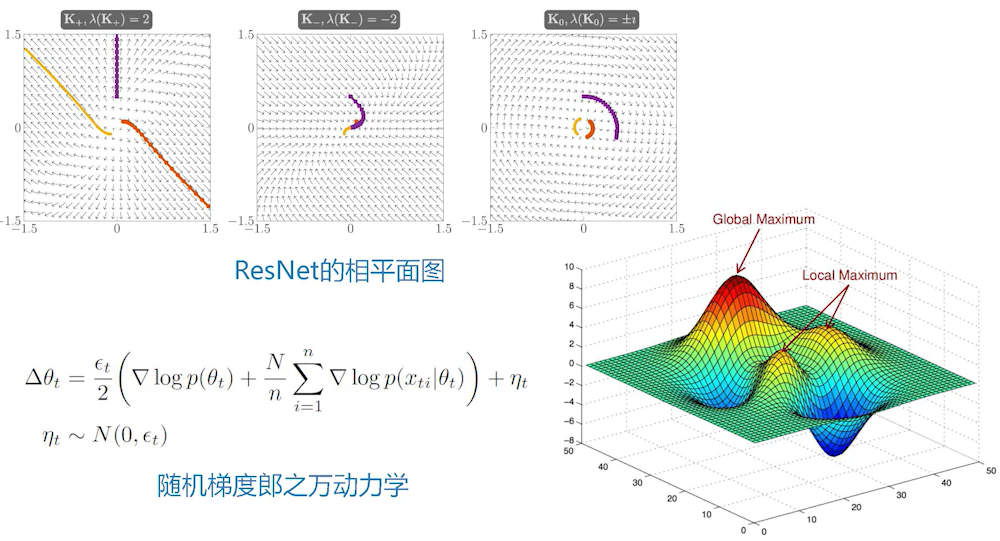
动力系统主要是指稳定性的内容。Stable Architectures for Deep Neural Networks这篇文章是用相平面图来研究ResNet里面动力学的稳定性。
随机动力系统。比如:随机梯度下降。如果把它加一个人为的噪声($\eta{t} \sim N\left(0, \epsilon{t}\right)$),变成带噪声的迭代,叫“随机梯度郎之万动力学”,会带来一些更好的表现。
统计物理与非线性科学
平均场方法
平均场论(Mean field theory)是一种研究复杂多体问题的方法,将数量巨大的互相作用的多体问题转化成每一个粒子处在一种弱周期场中的单体问题。以平均作用效果替代单个作用效果的加和。
混沌和分形
混沌是时间上的分形,分形是空间上的混沌。
混沌和分形都是动力系统中非线性方程所描述的非平衡的过程和结果。
一些相关工作
A Mean Field View of the Landscape of Two-Layers Neural Networks
Hausdorff Dimension, Stochastic Differential Equations, and Generalization in Neural Networks
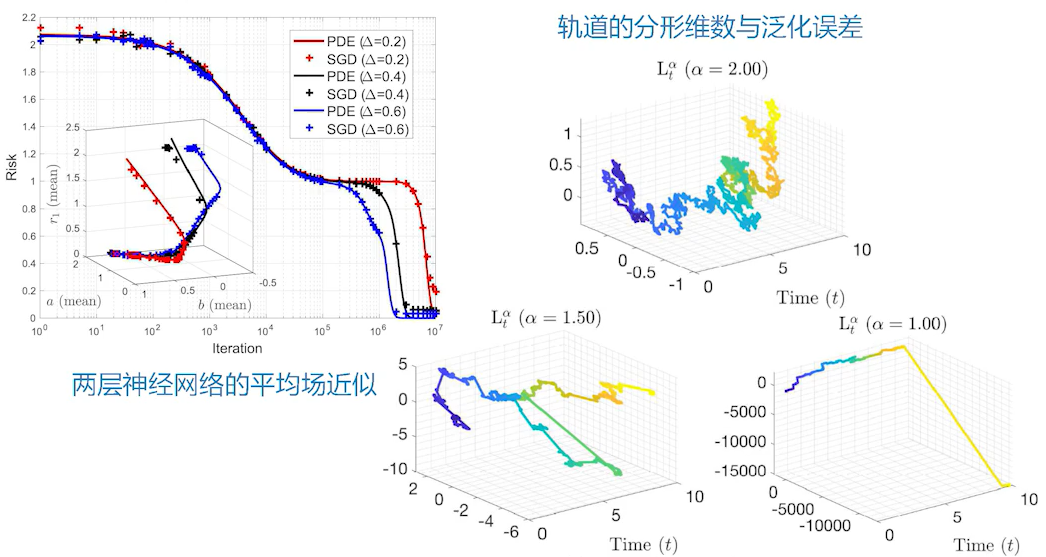
最近有这样一个工作,两层神经网络可以做一个平均场近似,平均场方法几乎是物理学家的法宝,任何情况下都可以做一个平均场近似,大部分情况下都 work 得比较好。对于两层无穷宽的神经网络,我们可以平均掉一些效果,这就可以得到一个比较好的跟实际效果吻合的预测。
非线性研究里还有很多研究混沌、分形几何之类的。举例来说,上图第二项工作是用随机梯度下降训练的轨道的分形维数来控制复杂度,由此可以得到一些泛化。
信息论
信息瓶颈方法
数据可能很多,将数据全部接收后进行压缩,称为信息瓶颈方法。可以用信息瓶颈方法来最优化地平衡准确度和复杂度。
信息瓶颈方法也用于分析深度学习的过程。
最大编码率降低原理
最大编码率降低原理(MCR2),这是一种信息理论度量,可以最大限度地提高整个数据集和每个类的编码率差。
相关工作
Opening the Black Box of Deep Neural Networks via Information
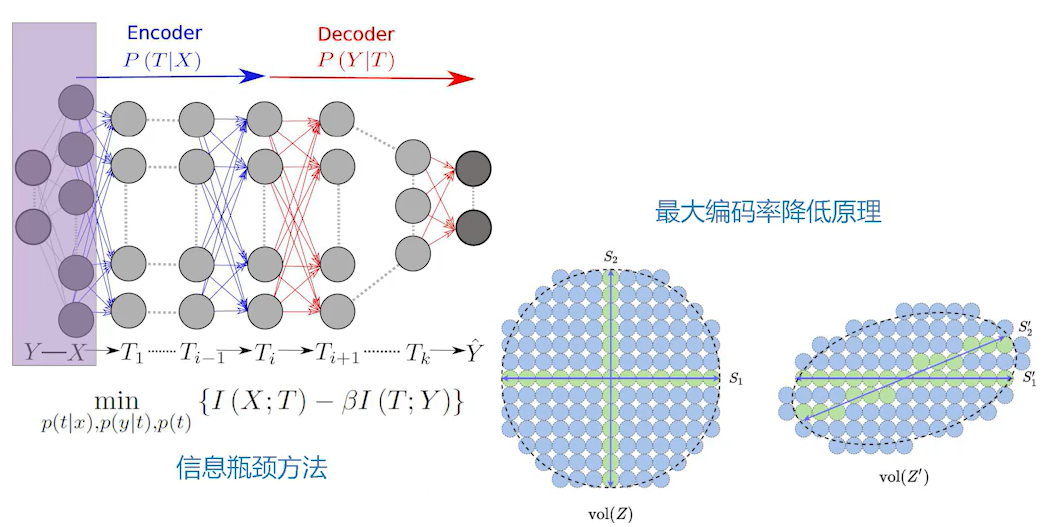
“信息瓶颈方法”,这是我们比较少接触的;还有“最大编码率降低原理”,是从信息论或者编码理论里面出来的一些方法。
博弈论
Shapley值法
合作博弈中分为:
- 功利主义:Shapley值
- 提倡最大化效益
- 平均主义:核
- 博弈的可行解空间构成一个核,核中任意一个分配都不会导致参与者组合脱离总合作
Shapley值衡量了一个联盟 $S$ 中参与者 $p_i$ 的边际贡献。
可解释性AI
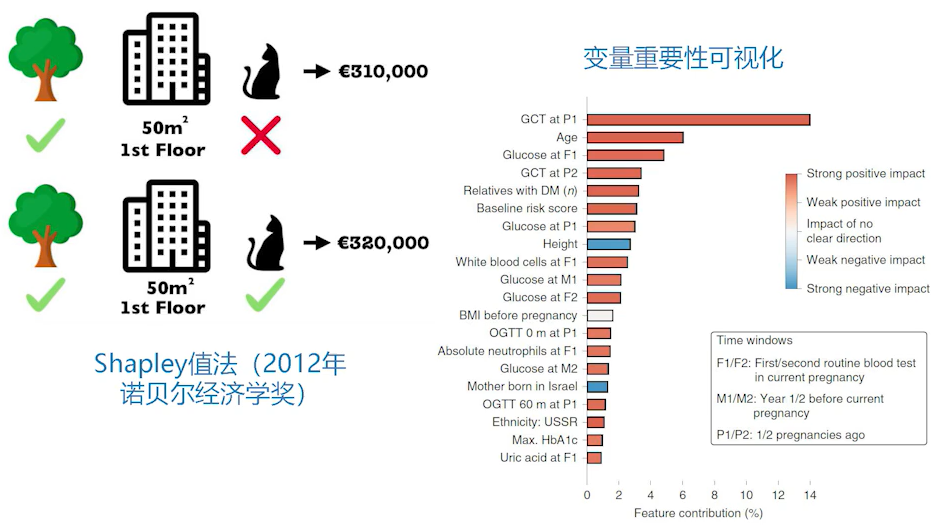
在可解释性AI里面有一个比较有名的方法叫Shapley值法。这个想法很简单,对一个黑箱的算法,要去看黑箱里的变量是怎么work的,以及哪些变量重要的。给它做一个可视化,可以假设这些变量之间在进行搏弈,在争夺对Response的某种payoff。在这个搏弈过程中,我们想办法把它们的贡献分配给这些变量。