思维之海

——在云端，寻找我的星匙。

欧拉回路拓展

In
欧拉回路相关知识。

Introduction

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。

如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。

具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

Application

欧拉回路的环扩展算法

Introduction

Ex：POJ1392：Ouroboros Snake【欧拉回路】

简要题意：

构造一个$2^n$位的循环数组，满足：

​ 每次从中截取n位，能够遍历所有的n位2进制数。

如：0110数组，将遍历：01，11，10，00。

可以采用DFS的方法。

@欧拉回路：

每个点的入度=出度，则该图存在欧拉回路。

示例：（4阶图）

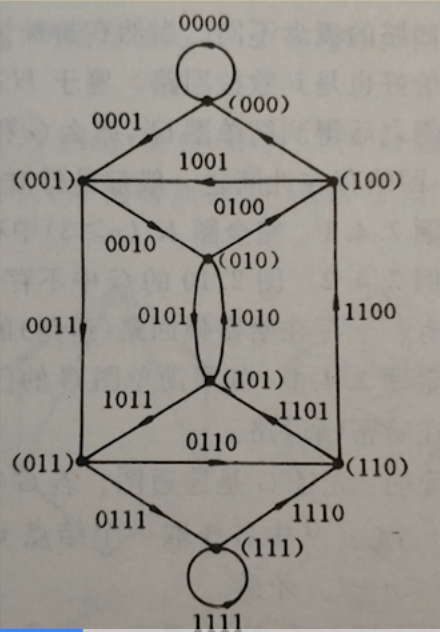
1533738094266

实际测试

先看dfs放在前和后的实际效果。（以n=3为例）

如下图所示：

两种的实际区别

使用的测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//allOne = 2^(n-1) - 1 = 100.. - 1 = 0111.. 
//vis:vis[i][u]表示从u出发值为i的边 (初始须置0状态，bool型)
//ans:答案 （初始须置0状态，string型）
//u：当前所在节点，2^(n-1)个 
//求欧拉回路，欧拉回路一定存在【入度=出度】 
void dfs(int u, int dex = 0) {
    for(int r = 0; r < dex; ++r) cout<<"  "; 
    cout<<"节点"<<bitset<3>(u)<<":"<<endl; 
    for(int i = 0; i <= 1; ++i) //兵分两路 
        if(!vis[i][u]) {
            int v = ((u << 1) | i) & allOne;    //将u左移一位，然后将最低位置为i，再将最高位去掉 
            vis[i][u] = 1;
            
            dfs(v, dex + 1);    //递归v，加入数字到ans中
            
            ans.push_back('0' + i);
            cout<<char('0' + i)<<endl;
            
            //dfs(v, dex + 1);    //后递归测试 
            }
}

测例分析

对本题基本的分析

声明：以下的所有讨论，除非特殊说明，“环”均不包括一个点的自环。（即，忽略000..和111..的自环）

我们建立n=3时的欧拉图。

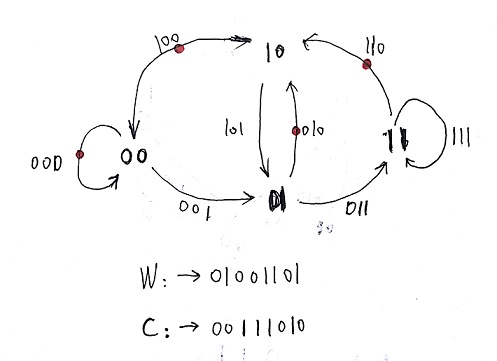
685751974715009958

可以看到

  • 两者点的遍历顺序一致。

  • 对于后DFS[先记录]，它的性质是真正的DFS。

    观察序列W(Wrong)：01001101，可以看到从00点开始，先搜索自己【000边】，再搜索001边，接着从01点继续深度搜索10点……

    此时，因为是先记录，可能会提前成环。即：路径0100。（DFS返回了00点）而本题的子环是相当密集的。

    DFS最终形成的是一棵搜索树。

    ​ 考虑DFS过程中可能出现的Backward边（子->父），即可扩展定义环。

    联想忒修斯的绳索。这里从略。

  • 对于前DFS[后记录]，它的性质才是欧拉图所要求的。这里称为“环扩展算法”。

    观察序列C(Correct)：00111010。

    第一个环：00-01-10-00，第二个环：01-11-10-01。

    我们发现一个奇妙的性质：

    ​ 对于n=3的欧拉图，整个欧拉图可以被分为两个环的(无重复)复合。

    ……我们是否可以推广这个结论呢？

验证、推广

给出n=4时的“环扩展算法”：

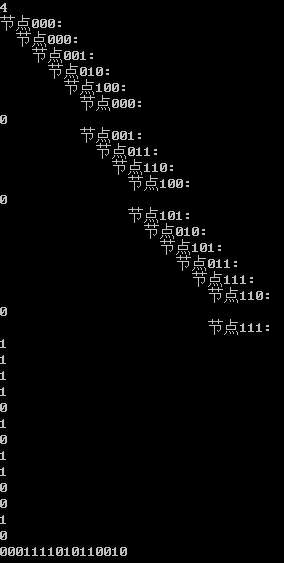
1530885513558

从图中我们可以直观地得到n=4欧拉图被分成了3个子环。

最终理论

我们可以继续做更高阶的测试。

​ n=5，类似的，分成4个子环。

​ n=6，5个子环。

​ ……

从中我们可以得出一个重要推论：

N欧拉状态图可以被分为N-1个子环。

环扩展算法有效的原理

回到n=3时的欧拉图。

685751974715009958

第一个环：00-01-10-00，第二个环：01-11-10-01。

规律：

1.从00点出发(忽略自环)。

2.采取的策略——每次尽可能取0。

​ 该策略能保证，每次的路线总能回到出发点。

【这样的保证是直接由欧拉图的性质决定的，因为：所有点的出/入度为偶数，起点必为终点。】

（不严格的）证明：【需改进】

对于任意一个n位二进制序列。

从000..(n-1)节点开始（忽略自环）

​ 初始序列000..01(n)，左移。尽可能补0。

​ 序列中仅含1个1。显然，经n步可回至初始状态。

从图中移除所有已遍历的边，更新欧拉图。即，将第一个环等效地缩并为000..01(n-1)节点的自环。

000..01(n-1)节点将成为新的初始节点。

​ 初始序列000..011(n)，左移。尽可能补0。

……

共n-1轮。

实际上，以上的思路可以按欧拉图的性质简化为：

每轮都能成环，而更新的欧拉图（从图中去掉本轮的环）仍然具有欧拉图的性质，因此最终一定会遍历所有边。

加上两次自环：000..0(n)和111..1(n)。

此时所有n位2进制数被遍历。（假装）证毕233。

而且由于对称性，我们可以预测，第i个环和第n-i个环的长度是相同的。

分析：

对于n=3的情况（如上图），该过程可以描述为：

  • 从00点出发，先0自环，然后1到达01，接着0-0回到00。
  • 00点没有出路，顺移到其后继01点，继续，1-0-0回到01。此时遍历了所有边。
  • 由于两个子环互不干扰，可以按以下逻辑复合：
    • 第一个环：00-01-10-00，根据第二个环，可以展开01节点，用第二个环替代。（由于自环的展开是平凡的，这也成为我们忽略自环的一个原因）
    • 最终复合为：00-01-11-10-01-10-00。

Plus. 联想Graham扫描算法，内在逻辑似乎很相似。

解的不唯一性-展开节点

由于每一次的展开是不唯一的（可以从环的不同节点展开），可以预见到解法的不唯一性。环扩展算法只是找到了其中一种。

比如：（n=3）

  • 第一个环：00-01-10-00，第二个环01-11-10-01可以等效地看作10-01-11-10，于是也可以展开10节点，用第二个环替代。
  • 最终复合为：00-01-10-01-11-10-00。

改进

修改策略

将原来测试代码的“兵分两路”修改为逆向循环：

1
for(int i = 1; i >= 0; --i) //兵分两路

即，采用新策略：

每次尽可能取1。

可以发现一个非常奇妙的现象，如下图：（n=3）

1531016147457

我们可以继续测试：

n=4

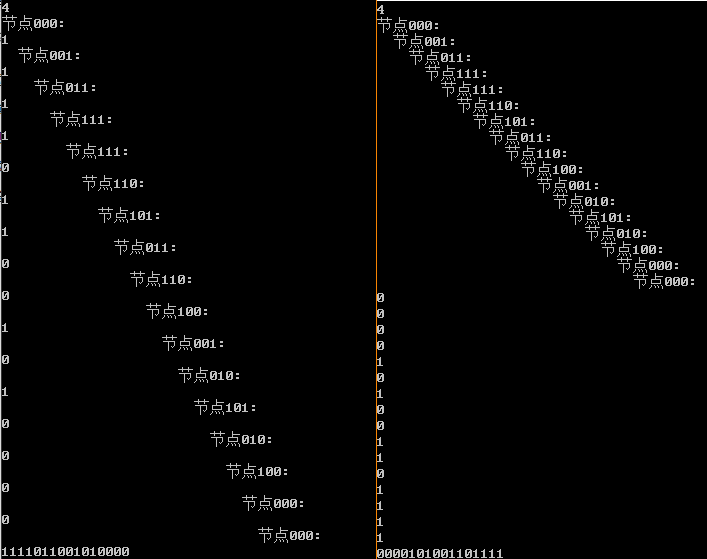
1531016307970

以及更高阶。（此处省略）

首先抛出结论：

对于新策略：

​ 每次尽可能取1。

前DFS（真）和后DFS（环扩展）的结果都是正确的，其结果是相反的。

（不严格的）证明：

对于每次尽可能取1的策略，我们可以合理地预测当所有路径没有被完全经历时，不可能提前回到000..节点。

因为：尽可能取1，意味着通向000..节点的0策略边必定是最后执行。

这样的分析可以推广到每一个节点：

对于$\forall$节点，其指向外界的0策略边必定是最后执行的。

从而证明了结论。

此时，可能会更加体会到两种方法（前/后）的根本区别。

这样的结果意味着什么呢？

分析

回到n=3，如下图：

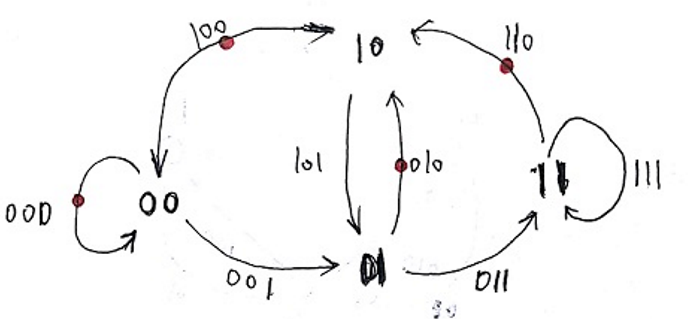
685751974715009958

我们来分析到底发生了什么。（也可以尝试自己先分析一下）

先给出每次尽可能取0的环扩展的线路图。红圈处为展开节点。绿圈为第1个环，粉圈为第2个环。

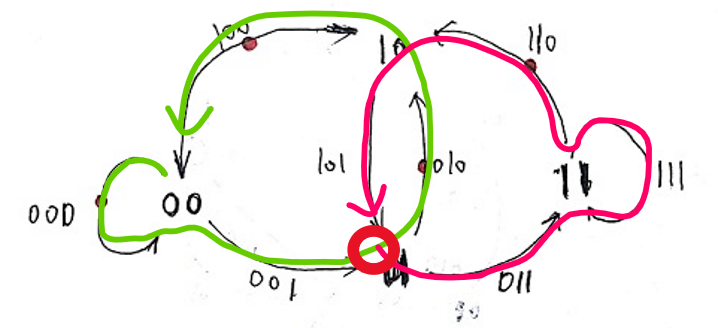
1531018156419

再给出每次尽可能取1的DFS的线路图。（两种方法的线路一致）

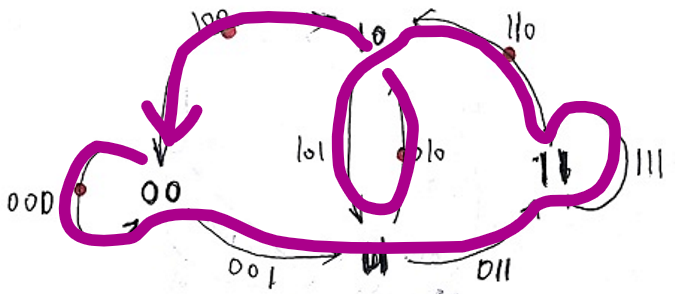
1531018570690

事实上，此时，DFS将一次就找到欧拉回路！因此前、后是等效的！

这两种策略的DFS对子环的划分是不同的。

对于每次尽可能取1的策略，其线路图可以等效地看作下图的一个划分【紫圈+蓝圈】。

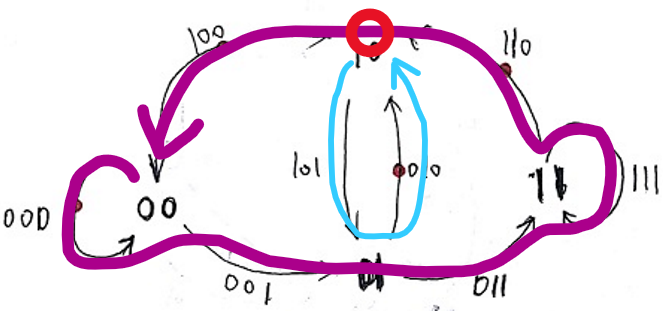
1531018948529

解的不唯一性-子环划分

事实上，对于n=3，在之前已经找到了两种路线：

  1. 00-01-11-10-01-10-00。（展开节点01）
  2. 00-01-10-01-11-10-00。（展开节点10）

若考虑子环划分的不同，我们将新增两种路线：（【紫+蓝】图）

  1. 00-01-11-10-01-10-00。（展开节点10）
  2. 00-01-10-01-11-10-00。（展开节点01）

容易看到，1、2与对应新增的3、4是完全一致的。这侧面映证了我们改进的思路是正确的。

此时，不同的子环划分，能够得出相同的多解。

仍然保证解的不唯一性。

拓展

更改初始节点

尝试进一步将原来测试代码的dfs初始节点设置为其他节点：

1
2
3
dfs(1);
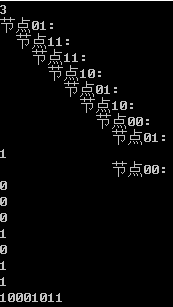
dfs(2);
dfs(3);

可以观察到以下：（n=3）

dfs(1);

1531023939934

dfs(2);

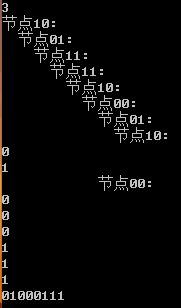
1531023748305

dfs(3); （结合环扩展算法的0优先策略，可以发现极强的对称性）

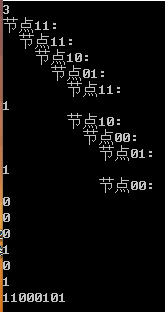
1531023787510

无论从哪个节点出发，均可以得到解！（更高阶不再赘述）

Plus. 不修改策略，也可以得到相同的结论。（但方法必须是环扩展，不是平凡~）

因此，

修改策略的实质是利用了0和1的对称性。

重要启发

但，这给了我们另一个重要的启发。

我们对所有n的情况，统一设置111..11节点为初始点。即

dfs($2^{n-1}-1$);

例如，n=3：

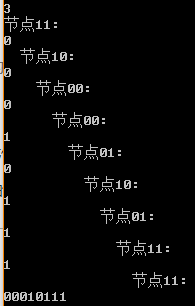
1531025354567

此时，平凡的DFS算法，又将得到正确解！

总结

采用前DFS的根本原因是：

本题的欧拉图是多环的。（此处，忽略000..和111..的自环）

搜索的迭代起始点是000..（111..等效），抗局部环干扰能力极弱。（只有1次进出机会）

​ 由于欧拉图多环，深度优先搜索不一定能在第一次就找到能遍历所有节点的环。

而我们的目的是：

找到遍历所有节点、边的广义环。

​ 因此，必须排除一切的局部环。

借助本题欧拉图的性质：

N欧拉状态图可以被划分为N-1个子环。（“划分”就是不多不少的分割）

或，N欧拉状态图可以被划分为N-1个环+2个自环。【考虑自环】

利用基于DFS改良的环扩展算法，即可求解N欧拉状态图。（多次复合）

利用基于策略的改进或更改初始节点，可以使得平凡的DFS算法也能得到正确解。（一次成功）

Reference

欧拉回路（百度百科）

初学算法之最基础的欧拉回路

[模板][持续更新]欧拉回路与欧拉路径浅析

uoj #117. 欧拉回路 圈套圈算法求欧拉回路